题目内容
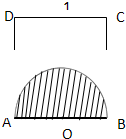
如图所示,以边长为1的正方形ABCD的一边AB为直径在其内部作一半圆.若在正方形中任取一点P,则点P恰好取自半圆部分的概率为( )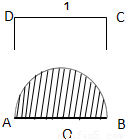
A.
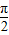
B.

C.
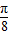
D.
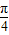
【答案】分析:根据题意,易得正方形OABC的面积,观察图形可得,阴影部分由半径为 的半圆围成,由面积公式,计算可得阴影部分的面积,进而由几何概型公式计算可得答案.
的半圆围成,由面积公式,计算可得阴影部分的面积,进而由几何概型公式计算可得答案.
解答:解:根据题意,正方形OABC的面积为1×1=1,
而阴影部分由半径为 的半圆围成,其面积为
的半圆围成,其面积为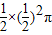 =
=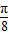 ,
,
则正方形OABC中任取一点P,点P取自阴影部分的概率为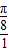 =
=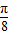 ;
;
故选C.
点评:本题考查几何概型的计算,涉及圆的面积在求面积中的应用,关键是正确计算出阴影部分的面积.
 的半圆围成,由面积公式,计算可得阴影部分的面积,进而由几何概型公式计算可得答案.
的半圆围成,由面积公式,计算可得阴影部分的面积,进而由几何概型公式计算可得答案.解答:解:根据题意,正方形OABC的面积为1×1=1,
而阴影部分由半径为
 的半圆围成,其面积为
的半圆围成,其面积为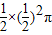 =
=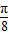 ,
,则正方形OABC中任取一点P,点P取自阴影部分的概率为
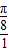 =
=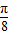 ;
;故选C.
点评:本题考查几何概型的计算,涉及圆的面积在求面积中的应用,关键是正确计算出阴影部分的面积.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
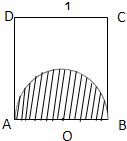 如图所示,以边长为1的正方形ABCD的一边AB为直径在其内部作一半圆.若在正方形中任取一点P,则点P恰好取自半圆部分的概率为( )
如图所示,以边长为1的正方形ABCD的一边AB为直径在其内部作一半圆.若在正方形中任取一点P,则点P恰好取自半圆部分的概率为( )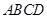 的一边
的一边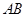 为直径在其内部作一半圆。若在正方形中任取一点
为直径在其内部作一半圆。若在正方形中任取一点 ,则点
,则点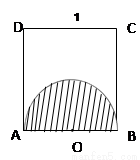
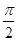 B.
B.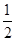
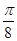 D.
D.