题目内容
求过点P(6,-4)且被圆x2+y2=20截得长为6| 2 |
分析:设出直线的斜率写出直线方程,然后求出圆心到直线的距离d,因为圆的半弦长、半径、弦心距恰好构成Rt△,根据勾股定理列出方程求出k的值代入弦所在的直线方程即可.
解答: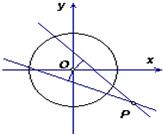 解:设弦所在的直线方程为y+4=k(x-6),即kx-y-6k-4=0①
解:设弦所在的直线方程为y+4=k(x-6),即kx-y-6k-4=0①
则圆心(0,0)到此直线的距离为d=
.
因为圆的半弦长、半径、弦心距恰好构成Rt△,
所以(
)2+(3
)2=20.
由此解得k=-
或k=-1.
代入①得:-
x-y-6×(-
)-4=0或-x-y-6×(-1)-4=0,即7x+17y+26=0或x+y-2=0.
 解:设弦所在的直线方程为y+4=k(x-6),即kx-y-6k-4=0①
解:设弦所在的直线方程为y+4=k(x-6),即kx-y-6k-4=0①则圆心(0,0)到此直线的距离为d=
| |6k+4| | ||
|
因为圆的半弦长、半径、弦心距恰好构成Rt△,
所以(
| |6k+4| | ||
|
| 2 |
由此解得k=-
| 7 |
| 17 |
代入①得:-
| 7 |
| 17 |
| 7 |
| 17 |
点评:此题是一道直线与圆的方程的综合应用题,要求学生掌握点到直线的距离公式和勾股定理的应用,以及会根据条件写出直线的一般式方程.

练习册系列答案
相关题目
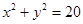 截得长为
截得长为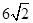 的弦所在的直线方程.
的弦所在的直线方程. ;(3)求过点P(3,-6)与函数f(x)的图像相切的直线方程。(12分)
;(3)求过点P(3,-6)与函数f(x)的图像相切的直线方程。(12分)
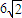 的弦所在的直线方程.
的弦所在的直线方程.