题目内容
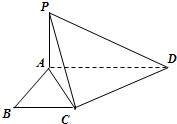 如图所示,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面ABCD.
如图所示,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面ABCD.(1)证明:PC⊥CD;
(2)若E是PA的中点,证明:BE∥平面PCD;
(3)若PA=3,求三棱锥B-PCD的体积.
分析:(1)要证明PC⊥CD,只需证明CD⊥平面PAC即可,即证明AC⊥CD,PA⊥CD;
(2)E是PA的中点,取AD的中点为F,连接BF,EF;要证明:BE∥平面PCD,只需证明平面BEF∥平面PCD即可.
(3)PA=3,求三棱锥B-PCD的体积,就是求P-BCD的体积,求出三角形BCD的面积,即可求解几何体的体积.
(2)E是PA的中点,取AD的中点为F,连接BF,EF;要证明:BE∥平面PCD,只需证明平面BEF∥平面PCD即可.
(3)PA=3,求三棱锥B-PCD的体积,就是求P-BCD的体积,求出三角形BCD的面积,即可求解几何体的体积.
解答: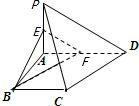 解:(1)由已知易得AC=
解:(1)由已知易得AC=
,CD=
.(1分)
∵AC2+CD2=AD2,
∴∠ACD=90°,即AC⊥CD.(2分)
又∵PA⊥平面ABCD,CD?平面ABCD,
∴PA⊥CD.(3分)
∵PA∩AC=A,
∴CD⊥平面PAC.(4分)
∵PC?平面PAC,
∴CD⊥PC.(5分)
(2)取AD的中点为F,连接BF,EF.
∵AD=2,BC=1,
∴BC∥FD,且BC=FD,
∴四边形BCDF是平行四边形,即BF∥CD.(6分)
∵BF?平面PCD,
∴BF∥平面PCD.(7分)
∵E,F分别是PA,AD的中点,
∴EF∥PD.
∵EF?平面PCD,
∴EF∥平面PCD.(9分)
∵EF∩BF=F,
∴平面BEF∥平面PCD.(10分)
∵EF?平面BEF,
∴BE∥平面PCD.(11分)
(3)由已知得S△BCD=
×1×1=
,(12分)
所以,VB-PCD=VP-BCD=
×PA×S△BCD=
×3×
=
.(14分)
 解:(1)由已知易得AC=
解:(1)由已知易得AC=| 2 |
| 2 |
∵AC2+CD2=AD2,
∴∠ACD=90°,即AC⊥CD.(2分)
又∵PA⊥平面ABCD,CD?平面ABCD,
∴PA⊥CD.(3分)
∵PA∩AC=A,
∴CD⊥平面PAC.(4分)
∵PC?平面PAC,
∴CD⊥PC.(5分)
(2)取AD的中点为F,连接BF,EF.
∵AD=2,BC=1,
∴BC∥FD,且BC=FD,
∴四边形BCDF是平行四边形,即BF∥CD.(6分)
∵BF?平面PCD,
∴BF∥平面PCD.(7分)
∵E,F分别是PA,AD的中点,
∴EF∥PD.
∵EF?平面PCD,
∴EF∥平面PCD.(9分)
∵EF∩BF=F,
∴平面BEF∥平面PCD.(10分)
∵EF?平面BEF,
∴BE∥平面PCD.(11分)
(3)由已知得S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
所以,VB-PCD=VP-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查线线垂直、线面平行、求锥体体积等立体几何知识,以及分析问题与解决问题的能力.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
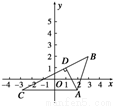
 如图所示,已知△ABC在第一象限,若A(1,1),B(5,1),A=60°,B=45°,求:
如图所示,已知△ABC在第一象限,若A(1,1),B(5,1),A=60°,B=45°,求: 如图所示,已知△ABC的水平放置的直观图是等腰直角△A′B′C′,∠A′=90°,
如图所示,已知△ABC的水平放置的直观图是等腰直角△A′B′C′,∠A′=90°, (2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
(2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB= 如图所示,已知△ABC中,AD是BC边上的中线,E是AD的中点,BE的延长线交AC于点F,则AF:AC=
如图所示,已知△ABC中,AD是BC边上的中线,E是AD的中点,BE的延长线交AC于点F,则AF:AC= 及点D的坐标.
及点D的坐标.