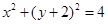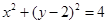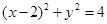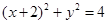题目内容
已知直线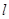 的参数方程:
的参数方程: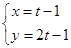
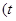 为参数
为参数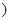 和圆
和圆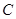 的极坐标方程:
的极坐标方程: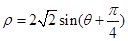
(1)将直线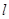 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆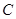 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)判断直线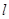 和圆
和圆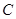 的位置关系.
的位置关系.
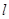 的参数方程:
的参数方程: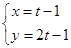
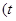 为参数
为参数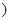 和圆
和圆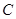 的极坐标方程:
的极坐标方程: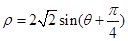
(1)将直线
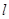 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆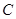 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;(2)判断直线
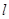 和圆
和圆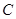 的位置关系.
的位置关系.(1)得⊙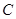 的直角坐标方程为:
的直角坐标方程为: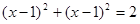
(2)直线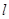 和⊙
和⊙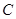 相交.
相交.
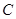 的直角坐标方程为:
的直角坐标方程为: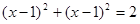
(2)直线
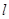 和⊙
和⊙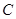 相交.
相交.(1)利用加减消参法得到直线l的普通方程,利用极坐标转化直角坐标公式的结论转化圆C的方程;(2)利用圆心到直线的距离与半径的比较判断直线与圆的位置关系。
(1)消去参数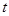 ,得直线
,得直线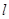 的普通方程为
的普通方程为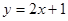 ;圆
;圆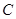 极坐标方程化为
极坐标方程化为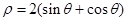 .两边同乘以
.两边同乘以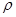 得
得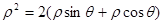 ,消去参数
,消去参数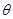 ,得⊙
,得⊙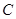 的直角坐标方程为:
的直角坐标方程为: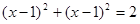 ……………… 4分
……………… 4分
(2)圆心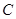 到直线
到直线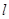 的距离
的距离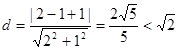 ,所以直线
,所以直线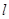 和⊙
和⊙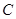 相交.
相交.
(1)消去参数
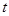 ,得直线
,得直线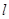 的普通方程为
的普通方程为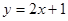 ;圆
;圆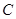 极坐标方程化为
极坐标方程化为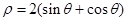 .两边同乘以
.两边同乘以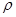 得
得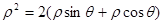 ,消去参数
,消去参数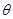 ,得⊙
,得⊙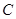 的直角坐标方程为:
的直角坐标方程为: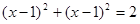 ……………… 4分
……………… 4分(2)圆心
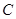 到直线
到直线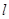 的距离
的距离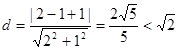 ,所以直线
,所以直线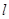 和⊙
和⊙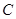 相交.
相交.
练习册系列答案
相关题目
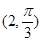 且与极轴垂直的直线方程为 ( )
且与极轴垂直的直线方程为 ( )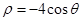
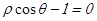
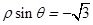
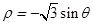
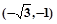 化为极坐标为( )
化为极坐标为( )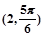
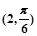
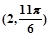
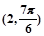
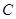 :
: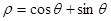 和直线
和直线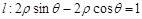 相交于
相交于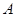 、
、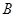 两点,求线段
两点,求线段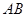 的长
的长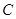 :
: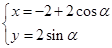 (
(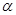 为参数),若以点
为参数),若以点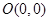 为极点,
为极点,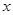 轴正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
轴正半轴为极轴建立极坐标系,则该曲线的极坐标方程是 .
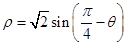 化为曲线的标准方程为 _________ .
化为曲线的标准方程为 _________ .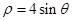 化为直角坐标方程为( )
化为直角坐标方程为( )