题目内容
设偶函数 满足
满足 (
( ),则
),则 =
=
 满足
满足 (
( ),则
),则 =
=A. | B. |
C. | D. |
B
试题分析:由偶函数满f(x)足f(x)=2x-4(x≥0),可得f(x)=f(|x|)=2|x|-4,根据偶函数的性质将函数转化为绝对值函数,再求解不等式,即由偶函数满足f(x)=2x-4(x≥0),可得f(x)=f(|x|)=2|x|-4,则f(x-2)=f(|x-2|)=2|x-2|-4,要使f(|x-2|)>0,只需2|x-2|-4>0,|x-2|>2
解得x>4,或x<0.应选B.
点评:解答本题的关键是利用偶函数的性质将函数转化为绝对值函数,从而简化计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
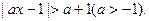
 则( ).
则( ).



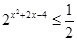 (2)计算
(2)计算
 的定义域为集合A,关于x的不等式
的定义域为集合A,关于x的不等式 的解集为B,求使
的解集为B,求使 的取值范围.
的取值范围. 的解集是 .
的解集是 . 上恒成立的正实数a的取值范围是_____________.
上恒成立的正实数a的取值范围是_____________.