题目内容
甲、乙两人在一场五局三胜制的象棋比赛中,规定甲或乙无论谁先赢满三局就获胜,并且比赛就此结束.现已知甲、乙两人每比赛一局甲取胜的概率是| 2 |
| 3 |
| 1 |
| 3 |
(Ⅰ)比赛以甲3胜1而结束的概率;
(Ⅱ)比赛以乙3胜2而结束的概率;
(Ⅲ)设甲获胜的概率为a,乙获胜的概率为b,求a:b的值.
分析:(I)每局比赛的胜负是独立的,这是一个相互独立事件同时发生的概率,比赛以甲3胜1而结束,则第四局一定甲胜,前三局中甲胜两局,写出概率.
(Ⅱ) 比赛以乙3胜2而结束,则第五局一定乙胜,前四局中乙胜两局,根据相互独立事件的概率和独立重复试验写出结果
(Ⅲ)甲先胜3局的情况有3种:3胜无败,3胜1败,3胜2败,这三种事件之间是互斥的,根据独立重复试验和互斥事件的概率公式得到结果.做出比值.
(Ⅱ) 比赛以乙3胜2而结束,则第五局一定乙胜,前四局中乙胜两局,根据相互独立事件的概率和独立重复试验写出结果
(Ⅲ)甲先胜3局的情况有3种:3胜无败,3胜1败,3胜2败,这三种事件之间是互斥的,根据独立重复试验和互斥事件的概率公式得到结果.做出比值.
解答:解:(Ⅰ)每局比赛的胜负是独立的,这是一个相互独立事件同时发生的概率,
比赛以甲3胜1而结束,则第四局一定甲胜,前三局中甲胜两局,
∴所求概率为:P=
×(
)2×
×
=
即比赛以甲3胜1而结束的概率为
.
(Ⅱ) 比赛以乙3胜2而结束,则第五局一定乙胜,前四局中乙胜两局,
∴所求概率为:P=
×(
)2×(
)2×
=
即比赛以乙3胜2而结束的概率为
(Ⅲ)甲先胜3局的情况有3种:3胜无败,3胜1败,3胜2败.这三种事件之间是互斥的,则其概率分别为
(
)3=
,
×(
)2×
×
=
,
×(
)2×(
)2×
=
,
于是甲获胜的概率a=
+
+
=
∴乙获胜的概率b=1-a=
∴a:b=64:17.
比赛以甲3胜1而结束,则第四局一定甲胜,前三局中甲胜两局,
∴所求概率为:P=
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 27 |
即比赛以甲3胜1而结束的概率为
| 8 |
| 27 |
(Ⅱ) 比赛以乙3胜2而结束,则第五局一定乙胜,前四局中乙胜两局,
∴所求概率为:P=
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 81 |
即比赛以乙3胜2而结束的概率为
| 8 |
| 81 |
(Ⅲ)甲先胜3局的情况有3种:3胜无败,3胜1败,3胜2败.这三种事件之间是互斥的,则其概率分别为
| C | 3 3 |
| 2 |
| 3 |
| 8 |
| 27 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 27 |
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 16 |
| 81 |
于是甲获胜的概率a=
| 8 |
| 27 |
| 8 |
| 27 |
| 16 |
| 81 |
| 64 |
| 81 |
∴乙获胜的概率b=1-a=
| 17 |
| 81 |
∴a:b=64:17.
点评:本题考查独立重复试验的概率,解题的关键是对于比赛的最后一局的结果是一个确定的结果,概率是1,这里容易出错.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 ,乙取胜的概率为
,乙取胜的概率为 ,且每局比赛的胜负是独立的,试求下列问题:
,且每局比赛的胜负是独立的,试求下列问题: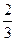 ,乙取胜的概率为
,乙取胜的概率为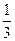 ,且每局比赛的胜负是独立的,试求下列问题:
,且每局比赛的胜负是独立的,试求下列问题: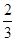 ,乙取胜的概率为
,乙取胜的概率为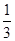 ,且每局比赛的胜负是独立的,试求下列问题:
,且每局比赛的胜负是独立的,试求下列问题: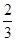 ,乙取胜的概率为
,乙取胜的概率为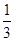 ,且每局比赛的胜负是独立的,试求下列问题:
,且每局比赛的胜负是独立的,试求下列问题: