题目内容
记函数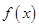 的导数为
的导数为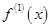 ,
,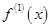 的导数为
的导数为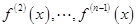 的导数为
的导数为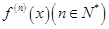 。若
。若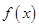 可进行
可进行 次求导,则
次求导,则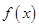 均可近似表示为:
均可近似表示为:
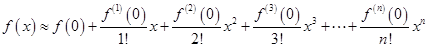
若取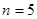 ,根据这个结论,则可近似估计自然对数的底数
,根据这个结论,则可近似估计自然对数的底数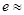 _____(用分数表示).
_____(用分数表示).
【答案】
 ;
;
【解析】
试题分析:构造函数f(x)=ex,根据导数运算,可知f(n)(x)=ex,f(n)(0)=1
所以若取n=5,ex≈f(0)+x+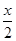 +
+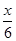 +
+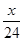 +
+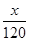 ,
,
令x=1,则e≈1+1+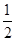 +
+ +
+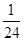 +
+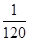 =
= ,故答案为
,故答案为 。
。
考点:本题主要考查导数的运算.
点评:本题综合考查函数求导运算,阅读、转化、构造、计算能力.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
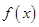 的导数为
的导数为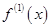 ,
,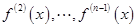 的导数为
的导数为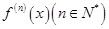 。若
。若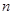 次求导,则
次求导,则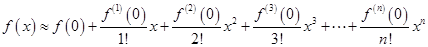
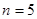 ,根据这个结论,则可近似估计自然对数的底数
,根据这个结论,则可近似估计自然对数的底数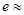 _____(用分数表示).
_____(用分数表示).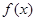 的导数为
的导数为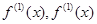 的导数为
的导数为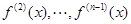 的导数为
的导数为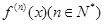 。若
。若
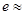 (用分数表示)
(用分数表示)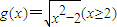 的导数为
的导数为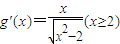 ,记函数f(x)=x-kg(x)(x≥2,k为常数).
,记函数f(x)=x-kg(x)(x≥2,k为常数).