题目内容

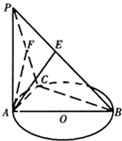如图，AB是⊙O的直径，C是圆周上不同于A、B的点，PA垂直于⊙O所在平面AE⊥PB于E，AF⊥PC于F，因此
AF
AF
⊥平面PBC（请填图上的一条直线）
分析：根据题意，BC⊥AC且BC⊥PA，结合线面垂直的判定定理，得到BC⊥平面PAC，从而得到平面PBC⊥平面PAC，而AF在平面PAC内且垂直于交线PC，联想平面与平面垂直的性质定理，得到AF⊥平面PBC，最后用直线与平面垂直的判定理可证出这个结论．
解答：解：∵PA⊥平面ACB，BC?平面ACB，
∴BC⊥PA
∵AB是⊙O的直径，
∴BC⊥AC，
∵PA∩AC=A，PA、AC?平面PAC
∴BC⊥平面PAC
∵AF?平面PAC
∴BC⊥AF
∵PC⊥AF，PC∩BC=B，PC、BC?平面PBC
∴AF⊥平面PBC
故答案为：AF
点评：本题给出一个探索性问题，通过寻找已知平面的垂线，着重考查了直线与平面垂直的判定与性质和平面与平面垂直的性质等知识点，属于中档题．
练习册系列答案
相关题目
（理科）如图的多面体是底面为平行四边形的直四棱柱ABCD-A1B1C1D1，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．
精英家教网
（Ⅰ）求证：BD⊥平面ADG；
（Ⅱ）求平面AEFG与平面ABCD所成锐二面角的余弦值．

（文科）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）设FC的中点为M，求证：OM∥平面DAF．
精英家教网

如图，已知PA垂直于⊙O所在平面，AB是⊙O的直径，点C为圆周上异于A、B的一点．

(1)若一个n面体中有m个面是直角三角形，则称这个n面体的直度为．那么四面体P－ABC的直度为多少？说明理由；

(2)在四面体P－ABC中，AP＝AB＝1，设．若动点M在四面体P－ABC表面上运动，并且总保持PB⊥AM．设为动点M的轨迹围成的封闭图形的面积关于角的函数，求取最大值时，二面角A－PB－C的正切值．

如图，已知PA垂直于⊙O所在平面，AB是⊙O的直径，点C为圆周上异于A、B的一点．

(1)若一个n面体中有m个面是直角三角形，则称这个n面体的直度为．那么四面体P－ABC的直度为多少？说明理由；

(2)如图，若四面体P－ABC中，AP＝AB＝1，AE⊥PB，垂足为E，AF⊥PC，垂足为F．设∠EAF＝，为△AEF面积的函数，求取最大值时二面角A－PB－C的大小．
如图，ABCD是正方形，E、F分别是AD、BC边上的点，EF∥AB，EF交AC于点O，以EF为棱把它折成直二面角A-EF-D后，求证：不论EF怎样移动，∠AOC是定值.

 如图甲，已知PA垂直于⊙O所在平面，AB是⊙O的直径，点C为圆周上异于A、B的一点．

（1）若一个面体中有个面是直角三角形，则称这个面体的直度为．那么四面体的直度为多少？说明理由；

（2）在四面体中，，设．若动点在四面体 表面上运动，并且总保持．设为动点的轨迹围成的封闭图形的面积关于角的函数，求取最大值时,二面角的正切值．

 

 

 

 

 

 

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网