题目内容
已知 an=
(n∈N*),则在数列{ an}中的前30项中,最大项和最小项分别是第
n-
| ||
n-
|
10
10
项、第9
9
项.分析:由题意已知数列{an}的通项an=
(n∈N*),由于数列是特殊的函数所以可以利用对勾函数的单调性加以求解即可.
n-
| ||
n-
|
解答:解:∵an=an=
=
=1+
,
记函数f(n)=1+
,
函数f(n)的大致图象如图所示,
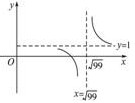
∴当n=10时,a10最大,
当n=9时,a9最小.
故答案为10,9.
n-
| ||
n-
|
n-
| ||||||
n-
|
| ||||
n-
|
记函数f(n)=1+
| ||||
n-
|
函数f(n)的大致图象如图所示,

∴当n=10时,a10最大,
当n=9时,a9最小.
故答案为10,9.
点评:此题考查了数列时特殊的函数,并联想利用对勾函数的单调及n∈N*进行求解.

练习册系列答案
相关题目