题目内容
(本小题9分)某家公司每月生产两种布料A和B,所有原料是三种不同颜色的羊毛,下表给出了生产每匹每种布料所需的羊毛量,以及可供使用的每种颜色的羊毛的总量。
已知生产每匹布料A、B的利润分别为120元、80元。那么如何安排生产才能够产生最大的利润?最大的利润是多少?
| 羊毛颜色 | 每匹需要 / kg | 供应量/ kg | |
| 布料A | 布料B | ||
| 红 | 4 | 4 | 1400 |
| 绿 | 6 | 3 | 1800 |
| 黄 | 2 | 6 | 1800 |
该公司每月生产布料A、B分别为250 、100匹时,产生最大的利润,最大的利润是38000 元。
本试题主要是考查了线性规划的运用,求解最优解问题的实际运用。
首先设每月生产布料A、B分别为x匹、y匹,利润为Z元,那么
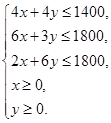 ①
①
目标函数为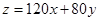
根据题意利用线性约束条件作出可行域,然后借助于图像,平移目标函数,得到目标函数的最优解。
设每月生产布料A、B分别为x匹、y匹,利润为Z元,那么
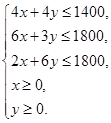 ①
①
目标函数为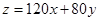
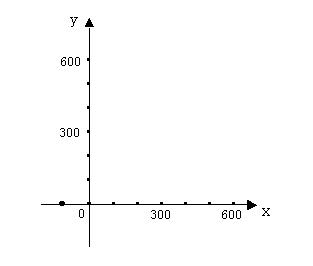
作出二元一次不等式①所表示的
平面区域(阴影部分)即可行域。

把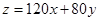 变形为
变形为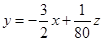 ,得到斜率为
,得到斜率为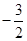 ,在轴上的截距为
,在轴上的截距为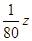 ,随z变化的一族平行直线。如图可以看出,当直线
,随z变化的一族平行直线。如图可以看出,当直线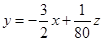 经过可行域上
经过可行域上
M时,截距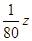 最大,即z最大。 解方程组
最大,即z最大。 解方程组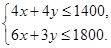 得M的坐标为x="250" , y=100 所以
得M的坐标为x="250" , y=100 所以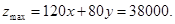
答:该公司每月生产布料A、B分别为250 、100匹时,产生最大的利润,最大的利润是38000 元。
首先设每月生产布料A、B分别为x匹、y匹,利润为Z元,那么
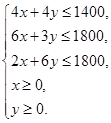 ①
① 目标函数为
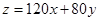
根据题意利用线性约束条件作出可行域,然后借助于图像,平移目标函数,得到目标函数的最优解。
设每月生产布料A、B分别为x匹、y匹,利润为Z元,那么
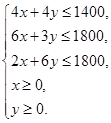 ①
① 目标函数为
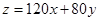
作出二元一次不等式①所表示的
平面区域(阴影部分)即可行域。


把
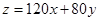 变形为
变形为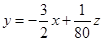 ,得到斜率为
,得到斜率为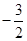 ,在轴上的截距为
,在轴上的截距为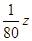 ,随z变化的一族平行直线。如图可以看出,当直线
,随z变化的一族平行直线。如图可以看出,当直线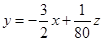 经过可行域上
经过可行域上M时,截距
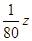 最大,即z最大。 解方程组
最大,即z最大。 解方程组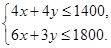 得M的坐标为x="250" , y=100 所以
得M的坐标为x="250" , y=100 所以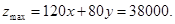
答:该公司每月生产布料A、B分别为250 、100匹时,产生最大的利润,最大的利润是38000 元。

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目

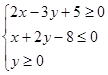 ,则目标函数
,则目标函数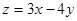 的最小值是_______.
的最小值是_______.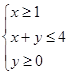 所表示的平面区域为
所表示的平面区域为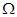 ,从
,从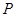 ,则点
,则点 ,
, 满足不等式组
满足不等式组 则
则 的最小值为
的最小值为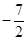



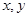 满足不等式组
满足不等式组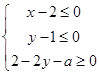 ,目标函数
,目标函数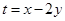 的最大值为2,则实数a的值是 ( )
的最大值为2,则实数a的值是 ( ) 满足约束条件
满足约束条件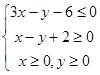 ,若目标函数
,若目标函数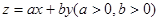 的最大值为12,则
的最大值为12,则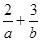 的最小值为 ;
的最小值为 ; 满足条件
满足条件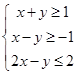 ,则目标函数
,则目标函数 的最大值是 .
的最大值是 .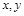 满足
满足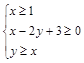 ,则
,则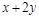 的最大值和最小值之和等于
的最大值和最小值之和等于