题目内容
.已知函数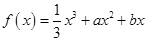 的极大值点为
的极大值点为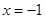 .
.
(1)用实数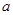 来表示实数
来表示实数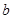 ,并求
,并求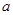 的取值范围;
的取值范围;
(2)当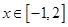 时,
时,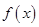 的最小值为
的最小值为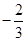 ,求
,求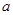 的值;
的值;
(3)设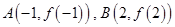 ,
,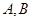 两点的连线斜率为
两点的连线斜率为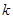 .求证:必存在
.求证:必存在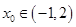 ,使
,使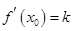 .
.
【答案】
解:(1)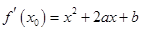 ,由题设知
,由题设知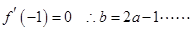 (2分)
(2分)
韦达定理得另一极点 ,因为
,因为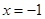 为极大值点
为极大值点
故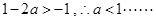 (4分)
(4分)
(2)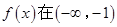 上递增,在
上递增,在 递减,在
递减,在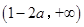 上递增,
上递增,
故当 时,分情况如下:
时,分情况如下:
当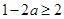 ,即
,即 时,
时, 在
在 上单调递减
上单调递减
 ,解得
,解得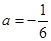 ,不合条件,舍去
,不合条件,舍去 (6分)
(6分)
当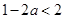 ,即
,即 时,
时,
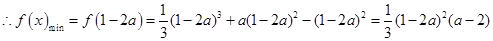
 ,化简得
,化简得 ,取
,取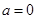 故所求的
故所求的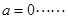 (9分)
(9分)
(3)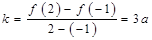 ,即证
,即证
即证方程 (
(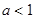 )在
)在 上有实数解,
上有实数解,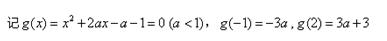
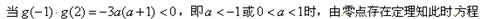 有解。
有解。
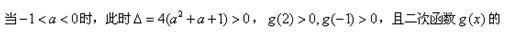
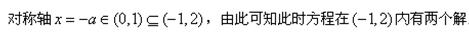
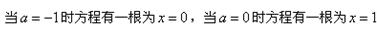
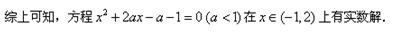
【解析】略

练习册系列答案
相关题目
 的极大值点和极小值点都在区间
的极大值点和极小值点都在区间 内,则实数
内,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 的极大值点和极小值点都在区间
的极大值点和极小值点都在区间 内,
内, ,2) D.
,2) D.
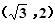
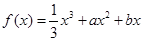 的极大值点为
的极大值点为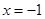 ,
,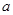 来表示实数
来表示实数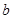 ,并求
,并求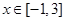 时,若
时,若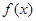 的最大值为6,求实数
的最大值为6,求实数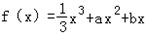 的极大值点为x=﹣1.
的极大值点为x=﹣1.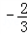 ,求a的值;
,求a的值;