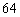题目内容
若 的二项展开式中,所有项的系数之和为64,则展开式中的常数项是 .
的二项展开式中,所有项的系数之和为64,则展开式中的常数项是 .
【答案】分析:依题意,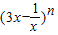 的二项展开式中,所有项的系数之和为64,就是x=1时的函数值,从而可求得n,利用其展开式的通项公式即可求得展开式中的常数项.
的二项展开式中,所有项的系数之和为64,就是x=1时的函数值,从而可求得n,利用其展开式的通项公式即可求得展开式中的常数项.
解答:解:依题意,当x=1时有2n=64,
∴n=6.设二项展开式的通项公式为:Tr+1=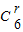 •(3x)6-r•(-x-1)r=(-1)r•36-r•
•(3x)6-r•(-x-1)r=(-1)r•36-r• •x6-r-r,
•x6-r-r,
∴由6-2r=0得r=3.
∴展开式中的常数项是T4=(-1)3•33• =-540.
=-540.
故答案为:-540.
点评:本题考查二项式定理的应用,由题意求得n=6是关键,着重考查二项展开式中的通项公式,属于中档题.
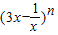 的二项展开式中,所有项的系数之和为64,就是x=1时的函数值,从而可求得n,利用其展开式的通项公式即可求得展开式中的常数项.
的二项展开式中,所有项的系数之和为64,就是x=1时的函数值,从而可求得n,利用其展开式的通项公式即可求得展开式中的常数项.解答:解:依题意,当x=1时有2n=64,
∴n=6.设二项展开式的通项公式为:Tr+1=
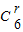 •(3x)6-r•(-x-1)r=(-1)r•36-r•
•(3x)6-r•(-x-1)r=(-1)r•36-r• •x6-r-r,
•x6-r-r,∴由6-2r=0得r=3.
∴展开式中的常数项是T4=(-1)3•33•
 =-540.
=-540.故答案为:-540.
点评:本题考查二项式定理的应用,由题意求得n=6是关键,着重考查二项展开式中的通项公式,属于中档题.

练习册系列答案
相关题目