题目内容
在直角坐标系xOy中,直线l的参数方程为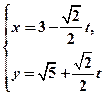 (t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为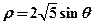
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B.若点P的坐标为(3,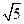 ),求|PA|+|PB|的值.
),求|PA|+|PB|的值.
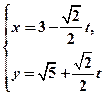 (t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为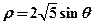
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B.若点P的坐标为(3,
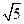 ),求|PA|+|PB|的值.
),求|PA|+|PB|的值.解:(1)由ρ=2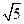 sinθ,得x2+y2-2
sinθ,得x2+y2-2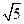 y=0,即x2+(y-
y=0,即x2+(y-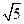 )2=5.。。。。。。。4分
)2=5.。。。。。。。4分
(2)解法一:将l的参数方程代入圆C的直角坐标方程,
得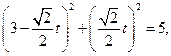
即t2-3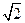 t+4=0.
t+4=0.
由于Δ=(3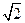 )2-4×4=2>0,
)2-4×4=2>0,
故可设t1,t2是上述方程的两实根,
所以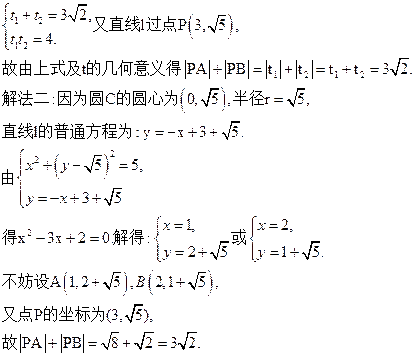
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。12分
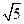 sinθ,得x2+y2-2
sinθ,得x2+y2-2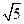 y=0,即x2+(y-
y=0,即x2+(y-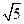 )2=5.。。。。。。。4分
)2=5.。。。。。。。4分(2)解法一:将l的参数方程代入圆C的直角坐标方程,
得
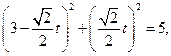
即t2-3
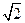 t+4=0.
t+4=0.由于Δ=(3
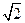 )2-4×4=2>0,
)2-4×4=2>0,故可设t1,t2是上述方程的两实根,
所以
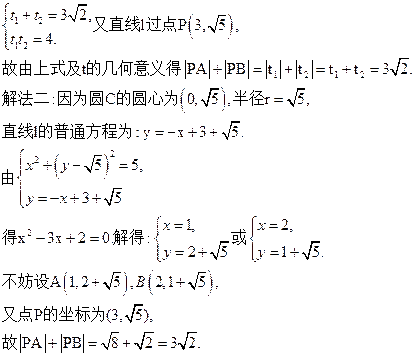
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。12分
略

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 的参数方程是
的参数方程是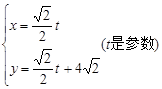 ,圆C的极坐标方程为
,圆C的极坐标方程为 .
.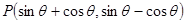 (
(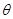 为参数)的轨迹方程是
为参数)的轨迹方程是
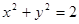
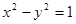
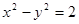
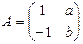 ,A的一个特征值
,A的一个特征值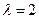 ,属于λ的特征向量是
,属于λ的特征向量是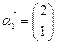 ,求矩阵A与其逆矩阵.
,求矩阵A与其逆矩阵.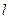 的极坐标方程是
的极坐标方程是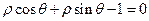 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为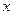 轴的正半轴,建立平面直角坐标系,在曲线
轴的正半轴,建立平面直角坐标系,在曲线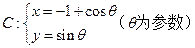 上求一点,使它到直线
上求一点,使它到直线 的参数方程是 ( )
的参数方程是 ( )



 系与
系与 参数方程
参数方程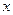 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位, 圆
轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位, 圆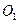 的方程为
的方程为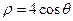 ,圆
,圆 的参数方程为
的参数方程为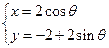 (为参数),求两圆的公共弦的长度。
(为参数),求两圆的公共弦的长度。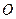 为极点,
为极点,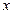 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点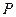 的直角坐标为
的直角坐标为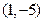 ,点
,点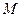 的极坐标为
的极坐标为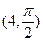 ,若直线
,若直线 过点
过点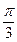 ,圆
,圆 以
以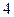 为半径。
为半径。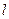 的参数方程是
的参数方程是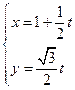 (t为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为
(t为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为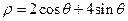 ,则直线
,则直线