题目内容

下列命题：
①若函数f（x）=x2-2x+3，x∈[-2，0]的最小值为3；
②线性回归方程对应的直线
?
y
=
?
b
x+
?
a
至少经过其样本数据点（x1，y1），（x2，y2），…，（xn，yn）中的一个点；
③命题p：?x＞0，x2+x+1＜0则￢p：?x＞0，x2+x+1≥0；
④若x1，x2，…，x10的平均数为a，方差为b，则2x1+5，2x2+5，…，2x10+5的平均数为2a+5，方差为4b．
其中，假命题的个数为（　　）
分析：①根据二次函数求最值的相关知识即可判断真假
②线性回归方程对应的直线
?
y
=
?
b
x+
?
a
是由最小二乘法计算出来的，它不一定经过其样本数据点
③根据写命题否定的原则，可判断真假
④根据平均数和方差的求解公式即可判断真假
解答：解：对于①：由题可知，函数f（x）=x2-2x+3，在x∈[-2，0]上单调递减
∴当x=0时取得最小值，最小值为f（0）=3
∴①是真命题
对于②：回归直线直线
?
y
=
?
b
x+
?
a
是由最小二乘法计算出来的，它不一定经过其样本数据点，一定经过(
.
x
，
.
y
)
∴②是假命题
对于③：存在性命题的命题写否定时，要改成全称命题
∴③是真命题
对于④：由求平均数和方差的公式可知，系数对平均数和方差
.
X
=
(2x1+5)+(2x2+5)+…+(2x10+5)
10
=
2×(x1+x2+…+x10)+10×5
10
=2a+5
方差S2=
(2x1+5-2a-5)2+(2x2+5-2a-5)2+…+(2x10+5-2a-5)2
10
=
(2x1-2a)2+(2x2-2a)2+…+(2x10-2a)2
10
=4×
(x1-a)2+(x2-a)2+…+(x10-a)2
10
=4b
∴④是真命题
∴假命题只有一个
故选B
点评：本题考查命题的真假性，要求对各个章节的知识点有比较扎实，比较全面的掌握．属简单题
练习册系列答案
相关题目
14、下列命题中：
①若函数f（x）的定义域为R，则g（x）=f（x）+f（-x）一定是偶函数；
②若f（x）是定义域为R的奇函数，对于任意的x∈R都有f（x）+f（2-x）=0，则函数f（x）的图象关于直线x=1对称；
③已知x1，x2是函数f（x）定义域内的两个值，且x1＜x2，若f（x1）＞f（x2），则f（x）是减函数；
④若f （x）是定义在R上的奇函数，且f （x+2）也为奇函数，则f （x）是以4为周期的周期函数．
其中正确的命题序号是
①④
．
下列命题中：
①若函数f（x）的定义域为R，则g（x）=f（x）+f（-x）一定是偶函数；
②直线x=
π
2
是函数y=sin（2x-
π
2
）图象的一条对称轴；
③若1，a，b，c，4这五个数组成一个等比数列，则b=±2；
④若实数x，y满足
x-y≤0
x-2y+2≥0
x≥-2
，则x+y的最大值是6；
其中正确的命题序号是
 
．
下列命题中：
①若函数f（x）的定义域为R，则g（x）=f（x）+f（-x）一定是偶函数；
②若f（x）是定义域为R的奇函数，对于任意的x∈R都有f（x）+f（2+x）=0，则函数f（x）的图象关于直线x=1对称；
③已知x1，x2是函数f（x）定义域内的两个值，且x1＜x2，若f（x1）＞f（x2），则f（x）是减函数；
④若f（x）是定义在R上的奇函数，且f（x+2）也为奇函数，则f（x）是以4为周期的周期函数．
其中正确的命题序号是
①④
①④
．
下列命题中：
①若函数f（x）的定义域为R，则g（x）=f（x）+f（-x）一定是偶函数；
②若f（x）是定义域为R的奇函数，对于任意的x∈R都有f（x）+f（2-x）=0，则函数f（x）的图象关于直线x=1对称；
③已知x1，x2是函数f（x）定义域内的两个值，且x1＜x2，若f（x1）＞f（x2），则f（x）是减函数；
④若f （x）是定义在R上的奇函数，且f （x+2）也为奇函数，则f （x）是以4为周期的周期函数．
其中正确的命题序号是    ．
下列命题中：
①若函数f（x）的定义域为R，则g（x）=f（x）+f（-x）一定是偶函数；
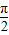②直线x=是函数y=sin（2x-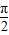）图象的一条对称轴；
③若1，a，b，c，4这五个数组成一个等比数列，则b=±2；
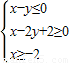④若实数x，y满足，则x+y的最大值是6；
其中正确的命题序号是    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网