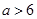题目内容
已知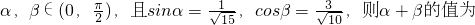
- A.

- B.
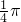
- C.
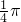 或
或
- D.2k
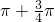
B
分析:根据条件和平方关系,求出cosα和sinβ的值,再利用两角和的余弦公式求cos(α+β)的值,再由α+β的范围求出它的值.
解答:∵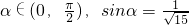 ,∴
,∴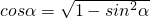 =
=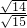 ,
,
∵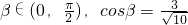 ,∴
,∴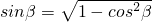 =
= ,
,
∴cos(α+β)=cosαcosβ-sinαsinβ=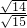 ×
× -
-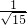 ×
× =
= ,
,
∵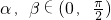 ,∴0<α+β<π,则α+β=
,∴0<α+β<π,则α+β= ,
,
故选B.
点评:本题是有关三角函数的化简求值题,根据平方关系求出对应角的正弦或余弦值,由两角和的余弦公式求所求角的余弦值,再判断范围求出对应角的值.
分析:根据条件和平方关系,求出cosα和sinβ的值,再利用两角和的余弦公式求cos(α+β)的值,再由α+β的范围求出它的值.
解答:∵
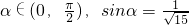 ,∴
,∴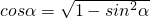 =
=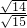 ,
,∵
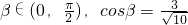 ,∴
,∴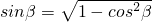 =
= ,
,∴cos(α+β)=cosαcosβ-sinαsinβ=
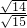 ×
× -
-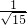 ×
× =
= ,
,∵
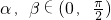 ,∴0<α+β<π,则α+β=
,∴0<α+β<π,则α+β= ,
,故选B.
点评:本题是有关三角函数的化简求值题,根据平方关系求出对应角的正弦或余弦值,由两角和的余弦公式求所求角的余弦值,再判断范围求出对应角的值.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
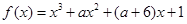 有极大值和极小值,则
有极大值和极小值,则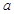 的取值范围是( )
的取值范围是( )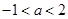 B.
B.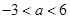 C.
C.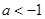 或
或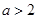 D.
D.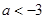 或
或