题目内容
已知函数g（x）=ax+2（a＞0），?x∈[-1，2]，使得g（x）∈[-1，3]，则实数a的取值范围是
- A.（0，
] - B.[，3]
- C.（0，3]
- D.[3，+∞）
D
分析：根据题意，可得-1≤ax+2≤3，从而可得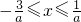
，利用?x∈[-1，2]，使得g（x）∈[-1，3]，即可求得实数a的取值范围．
解答：由题意，-1≤ax+2≤3
∴-3≤ax≤1
∴
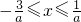
∵?x∈[-1，2]，使得g（x）∈[-1，3]，
∴
∴a≥3
故选D．
点评：本题考查特称命题，考查解不等式，考查学生的理解能力，属于中档题．
分析：根据题意，可得-1≤ax+2≤3，从而可得
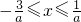，利用?x∈[-1，2]，使得g（x）∈[-1，3]，即可求得实数a的取值范围．解答：由题意，-1≤ax+2≤3
∴-3≤ax≤1
∴
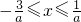
∵?x∈[-1，2]，使得g（x）∈[-1，3]，
∴
∴a≥3
故选D．
点评：本题考查特称命题，考查解不等式，考查学生的理解能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目