题目内容
如图所示，正方形ABCD是以金属丝围成的，其边长AB=1，把此正方形的金属丝重新围成扇形的A1D1C1，使A1D1=AD，D1C1=DC，正方形面积P，扇形面积Q，那么P和Q的大小关系是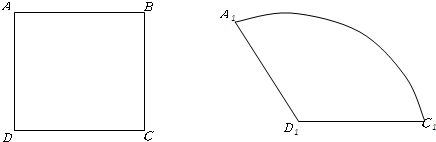
- A.P＜Q
- B.P=Q
- C.P＞Q
- D.无法确定
B
分析：先求出正方形的面积P，然后利用扇形的面积公式求出Q，然后比较两者的大小关系即可．
解答：一样大，正方形面积P=AB×AB=1 扇形面积Q=
lr=×2×1=1，
其中l为扇形弧长，等于正方形2个边长，r为扇形半径，等于正方形边长
∴P=Q
故选B．
点评：本题主要考查了函数模型的选择与应用，同时考查了扇形面积的度量，属于中档题．
分析：先求出正方形的面积P，然后利用扇形的面积公式求出Q，然后比较两者的大小关系即可．
解答：一样大，正方形面积P=AB×AB=1 扇形面积Q=
lr=×2×1=1，其中l为扇形弧长，等于正方形2个边长，r为扇形半径，等于正方形边长
∴P=Q
故选B．
点评：本题主要考查了函数模型的选择与应用，同时考查了扇形面积的度量，属于中档题．
练习册系列答案
相关题目
如图所示，正方形ADEF与梯形ABCD所在的平面互相垂直，AD⊥CD，AB∥CD，CD=2AB=2AD．
如图所示，直线AB的方程为6x-3y-4=0，向边长为2的正方形内随机地投飞镖，飞镖都能投入正方形内，且投到每个点的可能性相等，则飞镖落在阴影部分（三角形ABC的内部）的概率是（ ）
（2012•金华模拟）如图所示的正方形中，将边AB、AD各4等分，分别作AB、AD的平行线段成4×4方格网，则从图中取出一由网格线形成的矩形，恰好为正方形的概率是
如图所示，正方形AA1D1D与矩形ABCD所在平面互相垂直，AB=2AD=2，点E为AB的中点．