题目内容
设地球的半径为R，已知地球表面上A、B两地的纬度均为北纬45°，又A、B两地的球面距离为
R，则A、B两地的经度差可以为（ ）
| π |
| 3 |
| A、45° | B、60° |
| C、90° | D、120° |
分析：要求A，B两地的经度之差的绝对值，需要求出过A、B两点的小圆的圆心角的大小，利用题目条件进行转化，解三角形即可．
解答：解：地球半径为R，A、B两地均在北纬45°圈上，
过A、B两点的小圆的半径是：
两地的球面距离为
，所以AB=R
则A，B两地的经度之差的绝对值为：
故选C．
过A、B两点的小圆的半径是：
| ||
| 2 |
两地的球面距离为
| πR |
| 3 |
则A，B两地的经度之差的绝对值为：
| π |
| 2 |
故选C．
点评：本题考查球面距离及其计算，明确经度和纬度的含义，考查空间想象能力，解答关键是将空间问题转化为解平面几何中的三角形问题，是基础题．
练习册系列答案
相关题目
，若北半球的C地与A、B两地的球面距离均为
，则C地的纬度为
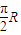，若A地为东经0°，则B地的经度为 ．