题目内容
已知正项数列{an}中，a1=6，点An(an，
)在抛物线y2=x+1上，数列{bn}中，点Bn(n，bn)
在过点(0，1)以(1，2)为方向向量的直线上．
(Ⅰ)求数列{an}，{bn}的通项公式；
(Ⅱ)若f(n)=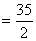
，问是否存在k∈N，使f(k+27)=4f(k)成立，若存在，求出k值；若不存在，请说明理由；
(Ⅲ)对任意正整数n，不等式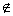
≤0恒成立，求正数a的取值范围．
答案：解：(1)a1=6, an+1=an+1.
∴an=6+(n-1)=n+5.
直线：y-1=2x y=2x+1过Bn(n，bn),
∴bn=2n+1.
(Ⅱ)f(n)=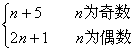
当k为奇数时，
f(k+27)=2(k+27)+1=4f(k)=4(k+5),
∴2k=35, kN.
当k为偶数时，
f(k+27)=k+27+5=4f(k)=4(2k+1),
7k=28, ∴k=4满足条件.
(Ⅲ)由条件知：a≤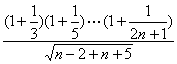
对n∈N*恒成立,
而f(n)=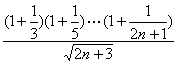
在[1，+∞)
上为增函数.
∴f(n)min=f(1)=
.
∴a≤
=
故a∈(0，
) .
练习册系列答案
相关题目