题目内容
设[x]表示不超过x的最大整数(如[2]=2,[1.3]=1),已知函数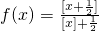 (x≥0),当f(x)<1时,实数x的取值范围是________.
(x≥0),当f(x)<1时,实数x的取值范围是________.
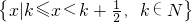
分析:由原不等式可得[x+
 ]<[x]+
]<[x]+ ,即[x+
,即[x+ ]-[x]<
]-[x]< ,故有
,故有 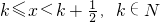 ,从而得出结论.
,从而得出结论.解答:f(x)<1,即
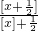 <1.
<1. 又 x≥0,∴[x+
 ]<[x]+
]<[x]+ ,即[x+
,即[x+ ]-[x]<
]-[x]< .
.设[x]=k,k∈N,则有 k≤x<k+1,且k≤x+
 <k+1.
<k+1.取交集可得
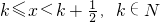 ,
,故答案为
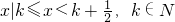 .
.点评:本题主要考查分式不等式的解法,注意[x]的意义,这是解题的易错点,属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
设[x]表示不超过x的最大整数(如[2]=2,[
]=1),对于给定的n∈N*,定义
=
,x∈[1,+∞),则当x∈[
,3)时,函数
的值域是( )
| 5 |
| 4 |
| C | x n |
| n(n-1)…(n-[x]+1) |
| x(x-1)…(x-[x]+1) |
| 3 |
| 2 |
| C | x 8 |
A、[
| ||||
B、[
| ||||
C、(4,
| ||||
D、(4,
|
设[x]表示不超过x的最大整数(如:[1]=1,[
]=2),则定义在[2,4)的函数f(x)=x[x]-ax(其中a为常数,且a≤4)的值域为( )
| 5 |
| 2 |
| A、[4-2a,64-4a) |
| B、[4-2a,9-3a)∪[27-3a,64-4a) |
| C、[9-3a,64-4a) |
| D、[4-2a,9-3a]∪(27-3a,64-4a] |
 =1),对于给定的n∈N+,定义
=1),对于给定的n∈N+,定义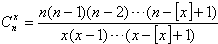 ,x∈[1,+∞),则
,x∈[1,+∞),则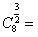 ( ),当x∈[2,3)时,函数
( ),当x∈[2,3)时,函数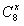 的值域是( )。
的值域是( )。