题目内容
【题目】从圆周的九等分点中,任取五点染为红色.证明:存在以红点为顶点的不同的六个三角形![]() ,满足
,满足![]() ,
,![]() ,
,![]() .
.
【答案】见解析
【解析】
注意如下事实:
(1)以![]() 、
、![]() 为底的等腰梯形
为底的等腰梯形![]() 中,存在两对全等三角形:
中,存在两对全等三角形:![]() ,
,![]() ,并且梯形的每个顶点都在其中一对全等三角形中两次出现.
,并且梯形的每个顶点都在其中一对全等三角形中两次出现.
(2)若![]() 是等腰梯形
是等腰梯形![]() 两底
两底![]() 、
、![]() 中垂线上的任一点,则
中垂线上的任一点,则![]() .
.
(i)先证明,五个红点中,必有某四点构成等腰梯形的四个顶点.
不妨设圆周上九等分点相邻两个分点间的弧长为1.再设一条弦,如果其所对的劣弧长为![]() ,则称该弦的“刻度”为
,则称该弦的“刻度”为![]() .于是,以分点为端点的弦的刻度只有1、2、3、4四种情况.显然,两弦相等当且仅当其刻度相等.五个红点共得
.于是,以分点为端点的弦的刻度只有1、2、3、4四种情况.显然,两弦相等当且仅当其刻度相等.五个红点共得![]() 条红端点的弦,其中必有三条弦具有相同的刻度,由于对每个
条红端点的弦,其中必有三条弦具有相同的刻度,由于对每个![]() ,同一点只能发出两条刻度为
,同一点只能发出两条刻度为![]() 的弦.注意到以九等分点为端点的任一条弦不为直径,因此,若两条等弦无公共端点,则其四个端点便构成等腰梯形的四个顶点.
的弦.注意到以九等分点为端点的任一条弦不为直径,因此,若两条等弦无公共端点,则其四个端点便构成等腰梯形的四个顶点.
若这三条等弦不围成三角形,则其中有两条等弦无公共端点.于是,其四个端点构成等腰梯形的四个顶点.
若这三条等弦围成三角形,则是正三角形.于是,这三条弦的刻度皆为3.若还有刻度为3的弦![]() ,则该弦与正三角形的每条边无公共端点.此时,弦
,则该弦与正三角形的每条边无公共端点.此时,弦![]() 与正三角形的每一条边所形成的四个端点都构成等腰梯形的四个顶点.若除了正三角形的边之外,再无刻度为3的弦,去掉这三条弦,剩下的7条弦只有1、2、4这三种刻度,其中必有三条弦具有相同的刻度,这三条等弦不可能围成三角形.因此,其中有两条等弦无公共端点.于是,其四个端点便构成等腰梯形的四个顶点.
与正三角形的每一条边所形成的四个端点都构成等腰梯形的四个顶点.若除了正三角形的边之外,再无刻度为3的弦,去掉这三条弦,剩下的7条弦只有1、2、4这三种刻度,其中必有三条弦具有相同的刻度,这三条等弦不可能围成三角形.因此,其中有两条等弦无公共端点.于是,其四个端点便构成等腰梯形的四个顶点.
(ii)由于弦的刻度只有1、2、3、4四种情况,故等腰梯形上下两底的“刻度对”只有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这六种可能,顺次如下图所示.
这六种可能,顺次如下图所示.
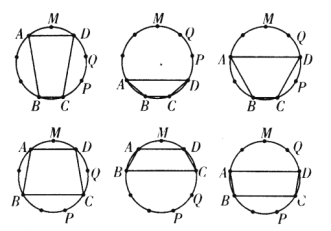
以下用梯形两底的刻度对表示相应的梯形图.
据(1)知,每个等腰梯形中都存在两对全等三角形.
再考虑第五个红点.
若该红点为两底中垂线上的点![]() ,据(2)知,存在另一对全等三角形
,据(2)知,存在另一对全等三角形![]() .
.
若该红点异于点![]() ,据图形的对称性,只需考虑红点为
,据图形的对称性,只需考虑红点为![]() 或
或![]() 的情况.再证明:无论增加红点
的情况.再证明:无论增加红点![]() 或
或![]() ,图形中都将新增一个等腰梯形.
,图形中都将新增一个等腰梯形.
i)若增加红点![]() ,则在图
,则在图![]() 中增加了梯形
中增加了梯形![]() ,在图
,在图![]() 中增加了梯形
中增加了梯形![]() ,在图
,在图![]() 中增加了梯形
中增加了梯形![]() ,在图
,在图![]() 中增加了梯形
中增加了梯形![]() ,在图
,在图![]() 中增加了梯形
中增加了梯形![]() ,在图
,在图![]() 中增加了梯形
中增加了梯形![]() .
.
ii)若增加红点![]() ,则在图
,则在图![]() 中增加了梯形
中增加了梯形![]() ,在图
,在图![]() 中增加了梯形
中增加了梯形![]() ,在图
,在图![]() 中增加了梯形
中增加了梯形![]() ,在图
,在图![]() 中增加了梯形
中增加了梯形![]() ,在图
,在图![]() 中增加了梯形
中增加了梯形![]() ,在图
,在图![]() 中增加了梯形
中增加了梯形![]() .
.
而据(1),新增红点必在新增梯形的一对全等三角形中两次出现,也就是增加了一对新的全等三角形.
因此,给出的五个红点中,存在六个以红点为顶点的三角形,它们可配成全等的三对.
故本题得证.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】“日行一万步,健康你一生”的养生观念已经深入人心,由于研究需要,某学生收集了“微信运动”中100名成员一天的行走步数,对这100个数据按组距为2500进行分组,并统计整理,绘制了如下尚不完整的统计表:
步数分组统计表(设步数为![]() )
)
组别 | 步数分组 | 频数 |
|
| 10 |
|
|
|
|
| 20 |
|
| 10 |
|
|
|
已知达到“日行一万步,健康你一生”标准的频率为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)以频率估计概率,从该“微信运动”中任意抽取3名成员,记其中达到“日行一万步,健康你一生”标准的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
