题目内容
方程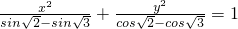 表示的曲线是
表示的曲线是
- A.焦点在x轴上的椭圆
- B.焦点在x轴上的双曲线
- C.焦点在y轴上的椭圆
- D.焦点在y轴上的双曲线
C
分析:先根据三角函数的单调性结合进而利用诱导公式可分别求得即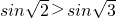 ,
,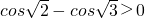 ,得出方程表示的曲线是椭圆.最后利用三角函数的单调性得到即
,得出方程表示的曲线是椭圆.最后利用三角函数的单调性得到即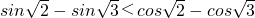 .从而曲线表示焦点在y轴上的椭圆.
.从而曲线表示焦点在y轴上的椭圆.
解答:∵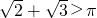 ,
,
∴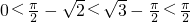 ,
,
∴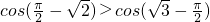 ,
,
即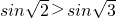 ,
,
又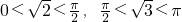 ,
,
∴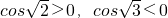 ,
,
∴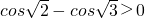 ,
,
方程表示的曲线是椭圆.
∵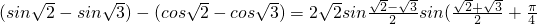 )(*)
)(*)
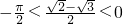 ,∴
,∴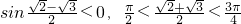 ,
,
∴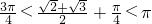 .∴
.∴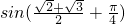 >0,∴(*)式<0.
>0,∴(*)式<0.
即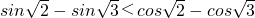 .∴曲线表示焦点在y轴上的椭圆,
.∴曲线表示焦点在y轴上的椭圆,
故选C.
点评:本题主要考查了圆锥曲线的共同特征,诱导公式的化简求值,椭圆的简单性质.解题的关键是找到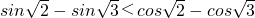 .
.
分析:先根据三角函数的单调性结合进而利用诱导公式可分别求得即
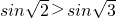 ,
,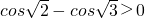 ,得出方程表示的曲线是椭圆.最后利用三角函数的单调性得到即
,得出方程表示的曲线是椭圆.最后利用三角函数的单调性得到即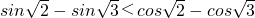 .从而曲线表示焦点在y轴上的椭圆.
.从而曲线表示焦点在y轴上的椭圆.解答:∵
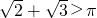 ,
,∴
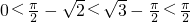 ,
,∴
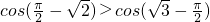 ,
,即
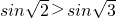 ,
,又
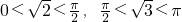 ,
,∴
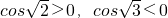 ,
,∴
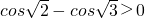 ,
,方程表示的曲线是椭圆.
∵
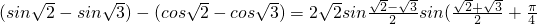 )(*)
)(*)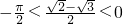 ,∴
,∴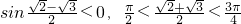 ,
,∴
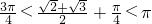 .∴
.∴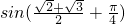 >0,∴(*)式<0.
>0,∴(*)式<0.即
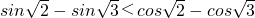 .∴曲线表示焦点在y轴上的椭圆,
.∴曲线表示焦点在y轴上的椭圆,故选C.
点评:本题主要考查了圆锥曲线的共同特征,诱导公式的化简求值,椭圆的简单性质.解题的关键是找到
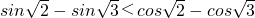 .
. 
练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
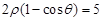 表示的曲线是 ( )
表示的曲线是 ( )