题目内容
已知与圆C:x2+y2-2x-2y+1=0相切的直线l交x轴,y轴于A,B两点,
OA|=a,|OB|=b(a>2,b>2).
(Ⅰ)求证:(a-2)(b-2)=2;
(Ⅱ)求线段AB中点的轨迹方程;
(Ⅲ)求△AOB面积的最小值.
OA|=a,|OB|=b(a>2,b>2).
(Ⅰ)求证:(a-2)(b-2)=2;
(Ⅱ)求线段AB中点的轨迹方程;
(Ⅲ)求△AOB面积的最小值.
(Ⅰ)见解析 (Ⅱ) (x-1)(y-1)=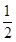 (x>1,y>1) (Ⅲ) 3+2
(x>1,y>1) (Ⅲ) 3+2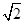
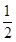 (x>1,y>1) (Ⅲ) 3+2
(x>1,y>1) (Ⅲ) 3+2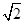
本题考查的知识点是直线和圆的方程的应用,轨迹方程,直线与圆的位置关系,考查的解题方法为坐标法,难度中等.
(1)由已知中圆C:x2+y2-2x-2y+1=0,直线交x轴、y轴于A、B两点|OA|=a,|OB|=b,我们设以分别求出直线的一般方程,和圆的标准方程,然后根据直线与圆相切,圆心到直线的距离等于半径得到结论;
(2)设线段AB的中点M(x,y),代入(1)的结论,整理后,即可得到答案;
(3)S△AOB=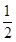 |ab|,结合(1)的结论,及均值不等式,即可得到答案.
|ab|,结合(1)的结论,及均值不等式,即可得到答案.
(Ⅰ)证明:圆的标准方程是(x-1)2+(y-1)2=1,设直线方程为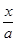 +
+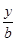 =1,即bx+ay-ab=0,圆心到该直线的距离d=
=1,即bx+ay-ab=0,圆心到该直线的距离d=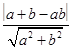 =1,………………………2分
=1,………………………2分
即a2+b2+a2b2+2ab-2a2b-2ab2=a2+b2,即a2b2+2ab-2a2b-2ab2=0,即ab+2-2a-2b=0,即(a-2)(b-2)=2.……………………………4分
(Ⅱ)设AB中点M(x,y),则a=2x,b=2y,代入(a-2)(b-2)=2,得(x-1)(y-1)=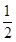 (x>1,y>1).……………………………………………………………8分
(x>1,y>1).……………………………………………………………8分
(Ⅲ)由(a-2)(b-2)=2得ab+2=2(a+b)≥4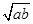 ,解得
,解得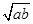 ≥2+
≥2+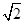 (舍去
(舍去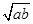 ≤2-
≤2-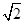 ),………………………………………………………………………10分
),………………………………………………………………………10分
当且仅当a=b时,ab取最小值6+4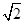 ,所以△AOB面积的最小值是3+2
,所以△AOB面积的最小值是3+2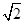 .…12分
.…12分
(1)由已知中圆C:x2+y2-2x-2y+1=0,直线交x轴、y轴于A、B两点|OA|=a,|OB|=b,我们设以分别求出直线的一般方程,和圆的标准方程,然后根据直线与圆相切,圆心到直线的距离等于半径得到结论;
(2)设线段AB的中点M(x,y),代入(1)的结论,整理后,即可得到答案;
(3)S△AOB=
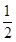 |ab|,结合(1)的结论,及均值不等式,即可得到答案.
|ab|,结合(1)的结论,及均值不等式,即可得到答案.(Ⅰ)证明:圆的标准方程是(x-1)2+(y-1)2=1,设直线方程为
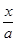 +
+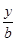 =1,即bx+ay-ab=0,圆心到该直线的距离d=
=1,即bx+ay-ab=0,圆心到该直线的距离d=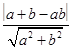 =1,………………………2分
=1,………………………2分即a2+b2+a2b2+2ab-2a2b-2ab2=a2+b2,即a2b2+2ab-2a2b-2ab2=0,即ab+2-2a-2b=0,即(a-2)(b-2)=2.……………………………4分
(Ⅱ)设AB中点M(x,y),则a=2x,b=2y,代入(a-2)(b-2)=2,得(x-1)(y-1)=
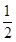 (x>1,y>1).……………………………………………………………8分
(x>1,y>1).……………………………………………………………8分(Ⅲ)由(a-2)(b-2)=2得ab+2=2(a+b)≥4
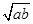 ,解得
,解得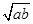 ≥2+
≥2+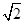 (舍去
(舍去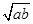 ≤2-
≤2-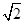 ),………………………………………………………………………10分
),………………………………………………………………………10分当且仅当a=b时,ab取最小值6+4
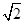 ,所以△AOB面积的最小值是3+2
,所以△AOB面积的最小值是3+2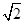 .…12分
.…12分
练习册系列答案
相关题目
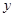 轴相切,圆心在直线
轴相切,圆心在直线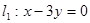 上,且在直线
上,且在直线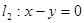 上截得的弦长为
上截得的弦长为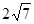 ,求圆C的方程.
,求圆C的方程. 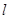 :
: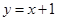 和圆C:
和圆C: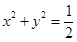 ,则直线
,则直线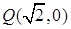 ,并且与定圆
,并且与定圆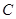 :
: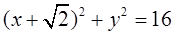 (圆心为C)相切.
(圆心为C)相切.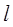 经过圆
经过圆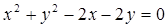 的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得
的圆心M,交动圆圆心P的轨迹于A、B两点.是否存在常数k,使得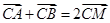 ?如果存在,求出
?如果存在,求出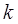 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.  与曲线
与曲线 (
( )有两个不同的公共点,则实数
)有两个不同的公共点,则实数 的取值范围为____________;
的取值范围为____________; 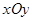 中,曲线
中,曲线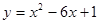 与坐标轴的交点都在圆
与坐标轴的交点都在圆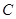 上.
上.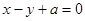 交于
交于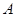 、
、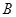 两点,且
两点,且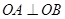 ,求
,求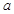 的值.
的值.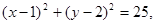

 取何实数,直线
取何实数,直线 与圆C恒相交;
与圆C恒相交;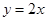 上一点
上一点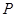 作圆
作圆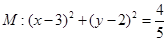 的两条切线
的两条切线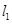 、
、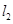 ,
,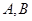 为切点,当
为切点,当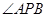 等于( )
等于( )



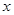 轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为
轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为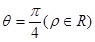 ,它与曲线
,它与曲线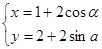 (
(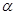 为参数)相交于两点A和B,则|AB|=______.
为参数)相交于两点A和B,则|AB|=______.