题目内容
已知{an}是以a为首项,q为公比的等比数列,Sn为它的前n项和,
(Ⅰ)当S1、S3、S4成等差数列时,求q的值;
(Ⅱ)当Sm、Sn、Sl成等差数列时,求证:对任意自然数k,am+k、an+k、al+k也成等差数列。
(Ⅰ)当S1、S3、S4成等差数列时,求q的值;
(Ⅱ)当Sm、Sn、Sl成等差数列时,求证:对任意自然数k,am+k、an+k、al+k也成等差数列。
解:(1)由已知,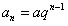 ,因此
,因此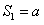 ,
,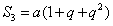 ,
,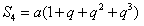 。当
。当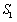 、S3、
、S3、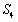 成等差数列时,
成等差数列时,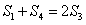 ,可得
,可得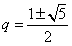
化简得 ,解得
,解得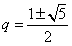 ;
;
(Ⅱ)若q=1,则{an}的每项an=a,此时 、
、 、
、 显然成等差数列;
显然成等差数列;
若 ,由Sm,Sn,Sl成等差数列可得
,由Sm,Sn,Sl成等差数列可得 ,即
,即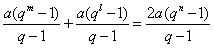
整理得 ,因此
,因此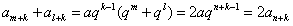
所以am+k,an+k,al+k也成等差数列。
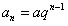 ,因此
,因此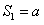 ,
,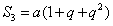 ,
,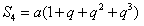 。当
。当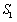 、S3、
、S3、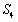 成等差数列时,
成等差数列时,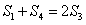 ,可得
,可得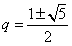
化简得
 ,解得
,解得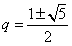 ;
;(Ⅱ)若q=1,则{an}的每项an=a,此时
 、
、 、
、 显然成等差数列;
显然成等差数列;若
 ,由Sm,Sn,Sl成等差数列可得
,由Sm,Sn,Sl成等差数列可得 ,即
,即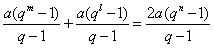
整理得
 ,因此
,因此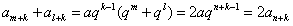
所以am+k,an+k,al+k也成等差数列。

练习册系列答案
相关题目