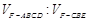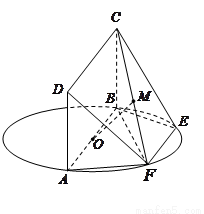题目内容
如图,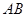 为圆
为圆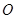 的直径,点
的直径,点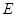 、
、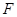 在圆
在圆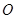 上,矩形
上,矩形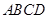 所在的平面和圆
所在的平面和圆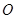 所在的平面互相垂直,且
所在的平面互相垂直,且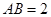 ,
,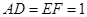 .
.

(Ⅰ)求证: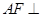 平面
平面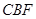 ;
;
(Ⅱ)求三棱锥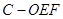 的体积.
的体积.
【答案】
(1)根据题意,由于平面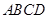
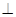 平面
平面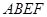 ,推理得到
,推理得到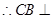 平面
平面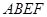 ,然后加以证明。
,然后加以证明。
(2)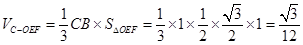
【解析】
试题分析:(Ⅰ)证明:平面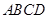
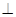 平面
平面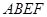 ,
, ,
,
平面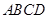
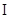 平面
平面 ,
,
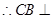 平面
平面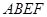 ,
,
∵AF在平面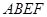 内,∴
内,∴ ,
3分
,
3分
又 为圆
为圆 的直径,∴
的直径,∴ ,
,
∴ 平面
平面 . 6分
. 6分
(Ⅱ)解:由(1)知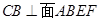 即
即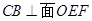 ,
,
∴三棱锥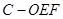 的高是
的高是 ,
,
∴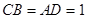 , 8分
, 8分
连结 、
、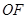 ,可知
,可知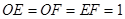
∴ 为正三角形,∴正
为正三角形,∴正 的高是
的高是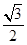 ,
10分
,
10分
∴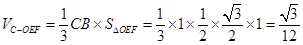 , 12分
, 12分

考点:线面垂直,棱锥的体积
点评:解决的关键是根据线面垂直度 判定定理和等体积法求解体积,属于基础题。

练习册系列答案
相关题目
 如图,
如图, 为圆
为圆 的直径,点
的直径,点 、
、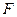 在圆
在圆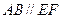 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 ,
, .
. 求证:
求证: 平面
平面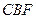 ;
;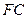 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
; 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为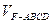 ,
,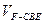 ,求
,求 .
.
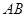 为圆
为圆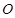 的直径,点
的直径,点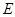 、
、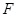 在圆
在圆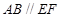 ,矩形
,矩形 的边
的边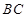 垂直于圆
垂直于圆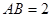 ,
,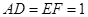 .
.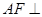 平面
平面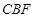 ;
; 的中点为
的中点为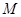 ,求证:
,求证: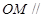 平面
平面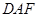 ;
;
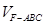 .
.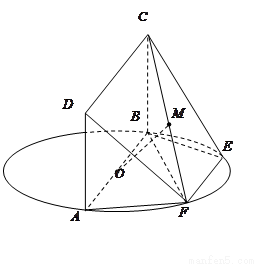
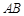 为圆
为圆 的直径,点
的直径,点 、
、 在圆
在圆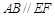 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 ,
, .
. 平面
平面 ;
; 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
;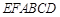 分成的两个锥体的体积分别为
分成的两个锥体的体积分别为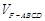 ,
, ,
,