题目内容
若一个四位数字的数,前两位数字之积恰好等于后面两位数,则称这个数为“吉积数”.如“0900”,“1909”,“9218”等都为“吉积数”.某地汽车牌照某批次的号码前两位是固定的英文字母,后面是四位数字,丁先生买了新车,给汽车上牌照时最多有三次选择机会(有放回地随机选择号码).丁先生选号时刚好是选这批号码的第一位,如果他想选一个末尾数字没有4的“吉积数”,则丁先生成功的最大概率最接近的值为( )A.3%
B.1%
C.0.88%
D.2.64%
【答案】分析:利用分布乘法计数原理求出这批汽车牌照某的号码的个数,利用列举的方法求出末尾数字没有4的“吉积数”的个数,利用古典概型的概率个数求出一次摸到末尾数字没有4的“吉积数”的概率,进一步求出丁先生成功的最大概率.
解答:解:这批汽车牌照某的号码共有10×10×10×10=104
末尾数字没有4的“吉积数”共有:
当前两位数中含0,的符合条件的数共有19个;
当前两位数中含1,的符合条件的数共有15个;
当前两位数中含2,的符合条件的数共有12个;
当前两位数中含3,的符合条件的数共有11个;
当前两位数中含4,的符合条件的数共有9个;
当前两位数中含5,的符合条件的数共有9个;
当前两位数中含6,的符合条件的数共有5个;
当前两位数中含7,的符合条件的数共有5个;
当前两位数中含8,的符合条件的数共有2个;
当前两位数中含9,的符合条件的数共有1个;
末尾数字没有4的“吉积数”共有:19+15+12+11+9+9+5+5+2+1=88
末尾数字没有4的“吉积数的概率为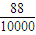
所以丁先生成功的最大概率最接近的值为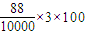 %=2.64%
%=2.64%
故选D.
点评:求一个事件的概率,关键是判断出事件的概型,然后选择合适的概率个数进行计算.
解答:解:这批汽车牌照某的号码共有10×10×10×10=104
末尾数字没有4的“吉积数”共有:
当前两位数中含0,的符合条件的数共有19个;
当前两位数中含1,的符合条件的数共有15个;
当前两位数中含2,的符合条件的数共有12个;
当前两位数中含3,的符合条件的数共有11个;
当前两位数中含4,的符合条件的数共有9个;
当前两位数中含5,的符合条件的数共有9个;
当前两位数中含6,的符合条件的数共有5个;
当前两位数中含7,的符合条件的数共有5个;
当前两位数中含8,的符合条件的数共有2个;
当前两位数中含9,的符合条件的数共有1个;
末尾数字没有4的“吉积数”共有:19+15+12+11+9+9+5+5+2+1=88
末尾数字没有4的“吉积数的概率为
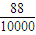
所以丁先生成功的最大概率最接近的值为
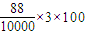 %=2.64%
%=2.64%故选D.
点评:求一个事件的概率,关键是判断出事件的概型,然后选择合适的概率个数进行计算.

练习册系列答案
相关题目
 如“0900”,“1909”,“9218”等都为“吉积数”。某地汽车牌照某批次的号码前两位是固定的英文字母,后面是四位数字,则这批号码中末位数字不为4的“吉积数”的概率为( )
如“0900”,“1909”,“9218”等都为“吉积数”。某地汽车牌照某批次的号码前两位是固定的英文字母,后面是四位数字,则这批号码中末位数字不为4的“吉积数”的概率为( ) B.0.0088
C.0.91
D.0.0091
B.0.0088
C.0.91
D.0.0091