题目内容
化简：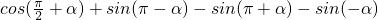
=________．
2sinα
分析：根据所给的函数式，要对函数进行整理求值，根据诱导公式把四项都变化成同一个角的三角函数形式，合并整理出最简结果．
解答：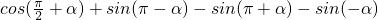
=-sinα+sinα+sinα+sinα=2sinα
故答案为：2sinα
点评：本题看出三角函数的化简求值即诱导公式的应用，本题解题的关键是正确利用诱导公式，不要在符号上出错，本题是一个基础题．
分析：根据所给的函数式，要对函数进行整理求值，根据诱导公式把四项都变化成同一个角的三角函数形式，合并整理出最简结果．
解答：
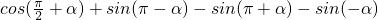
=-sinα+sinα+sinα+sinα=2sinα
故答案为：2sinα
点评：本题看出三角函数的化简求值即诱导公式的应用，本题解题的关键是正确利用诱导公式，不要在符号上出错，本题是一个基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知f（x）=
，当θ∈（
，
）时，f（sin2θ）-f（-sin2θ）可化简为（ ）
| 1-x |
| 5π |
| 4 |
| 3π |
| 2 |
| A、2sinθ |
| B、-2cosθ |
| C、-2sinθ |
| D、2cosθ |