题目内容
 (2013•安庆三模)如图,倾斜角为θ的直线OP与单位圆在第一象限的部分交于点P,单位圆与坐标轴交于点A(-1,0),点B(0,-1),PA与y轴交于点N,PB与x轴交于点M,设
(2013•安庆三模)如图,倾斜角为θ的直线OP与单位圆在第一象限的部分交于点P,单位圆与坐标轴交于点A(-1,0),点B(0,-1),PA与y轴交于点N,PB与x轴交于点M,设| PO |
| PM |
| PN |
(1)用角θ表示点M、点N的坐标;
(2)求x+y的最小值.
分析:(1)设P(cosθ,sinθ),N(0,t),
=λ
(λ为常数).由向量的坐标运算化简解出t=
,由此即可得到角θ表示点M、点N的坐标的表达式;
(2)由(1)得到向量
、
关于θ的坐标表示式,代入
=x
+y
得到关于θ、x、y的方程组,化简整理可得x+y=
=1+
,由此结合0<θ<
,即可算出x+y的最小值为
.
| AN |
| Ap |
| sinθ |
| 1+cosθ |
(2)由(1)得到向量
| PM |
| PN |
| PO |
| PM |
| PN |
| 2+sinθ+cosθ |
| 1+sinθ+cosθ |
| 1 | ||||
1+
|
| π |
| 2 |
| 2 |
解答:解:(1)设P(cosθ,sinθ),N(0,t)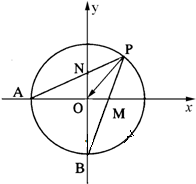
根据P、N、A共线,设
=λ
,(λ为常数) …①
又∵A(-1,0),∴
=(1,t),
=(cosθ+1,sinθ),
代入①,解得t=
,
∴N(0,
),同理可得M(
,0).…(4分)
(2)由(1)知
=(-cosθ,-sinθ),
=(
-cosθ,-sinθ)=(
,-sinθ),
=(-cosθ,
),…(6分)
代入
=x
+y
,得:
,
整理得:xsinθ+(1+sinθ)y=1+sinθ…②,(1+cosθ)x+ycosθ=1+cosθ…③.
②+③,解得:x+y=
=1+
=1+
,…(10分)
由点P在第一象限得0<θ<
,
所以当且仅当θ=
时,x+y的最小值为
. …(12分)

根据P、N、A共线,设
| AN |
| Ap |
又∵A(-1,0),∴
| AN |
| AP |
代入①,解得t=
| sinθ |
| 1+cosθ |
∴N(0,
| sinθ |
| 1+cosθ |
| cosθ |
| 1+sinθ |
(2)由(1)知
| PO |
| PM |
| cosθ |
| 1+sinθ |
| -sinθcosθ |
| 1+sinθ |
| PN |
| -sinθcosθ |
| 1+cosθ |
代入
| PO |
| PM |
| PN |
|
整理得:xsinθ+(1+sinθ)y=1+sinθ…②,(1+cosθ)x+ycosθ=1+cosθ…③.
②+③,解得:x+y=
| 2+sinθ+cosθ |
| 1+sinθ+cosθ |
| 1 |
| 1+sinθ+cosθ |
| 1 | ||||
1+
|
由点P在第一象限得0<θ<
| π |
| 2 |
所以当且仅当θ=
| π |
| 4 |
| 2 |
点评:本题在坐标系的单位圆中给出几何关系式,求用θ表示点M、点N的坐标表示式和x+y的最小值.着重考查了平面向量的坐标运算、在实际问题中建立三角函数模型和三角函数的化简求最值等知识,属于中档题.

练习册系列答案
相关题目