题目内容
如图，从圆O外一点A引圆的切线AD和割线ABC，已知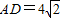
，圆O的半径r=AB=4，则圆心O到AC的距离为 ．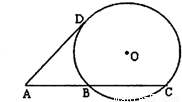
【答案】分析：设BC=x，由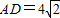
，圆O的半径r=AB=4，知
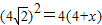，解得BC=x=4．故△OBC是边长为4的等边三角形，由此能求出圆心O到AC的距离．
解答：解：设BC=x，
∵
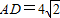，圆O的半径r=AB=4，
∴
，
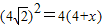解得BC=x=4．
∴△OBC是边长为4的等边三角形，
∴圆心O到AC的距离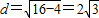
．
故答案为：2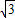
．
点评：本题考查与圆有关的比例线段，是基础题．解题时要认真审题，注意切割线定理的合理运用．
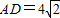，圆O的半径r=AB=4，知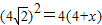，解得BC=x=4．故△OBC是边长为4的等边三角形，由此能求出圆心O到AC的距离．解答：解：设BC=x，
∵
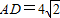，圆O的半径r=AB=4，∴
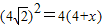，解得BC=x=4．
∴△OBC是边长为4的等边三角形，
∴圆心O到AC的距离
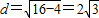．故答案为：2
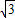．点评：本题考查与圆有关的比例线段，是基础题．解题时要认真审题，注意切割线定理的合理运用．
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
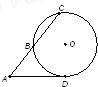如图，从圆O外一点A引圆的切线AD和割线ABC，已知AD=2
（几何证明选讲选做题）如图，从圆O外一点A引圆的切线AD和割线ABC，已知AC=6，圆O的半径为3，圆心O到AC的距离为
（2007•汕头二模）如图，从圆O外一点A引切线AD和割线ABC，AB=3，BC=2，则切线AD的长为
（考生注意：只能从下列A、B、C三题中选做一题，如果多做，则按第一题评阅记分）