题目内容
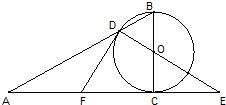 已知:在直角三角形ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,连接DO并延长交AC的延长线于点E,⊙O的切线DF交AC于F点.
已知:在直角三角形ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,连接DO并延长交AC的延长线于点E,⊙O的切线DF交AC于F点.(Ⅰ)试证明:AF=CF;
(Ⅱ)若ED=4,sin∠E=
| 3 | 5 |
分析:(Ⅰ)因为根据圆的切线知:FD=CF,要证AF=CF,只要证AF=FD即可,这个等式可以通过角∠A和∠ADF之间的关系得到证明三角形ADF是等腰三角形而得到;
(II)先在直角三角形FED中利用三角函数的边角关系求出FE,再利用线段之间的关系CE=FE-FC,求出CE即可.
(II)先在直角三角形FED中利用三角函数的边角关系求出FE,再利用线段之间的关系CE=FE-FC,求出CE即可.
解答:证明:(Ⅰ)设线段FD延长线上一点G,则∠GDB=∠ADF,且∠GDB+∠BDO=
,
∴∠ADF+∠BDO=
,(2分)
又∵⊙O中OD=OB,
∴∠BDO=∠OBD,
∴∠ADF+∠OBD=
,
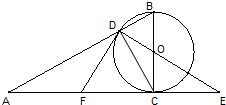 在Rt△ABC中,
在Rt△ABC中,
∴∠A+∠OBD=
,∠A=∠ADF,
∴AF=FD,
又在直角三角形ABC中,直角边BC为⊙O的直径,
∴AC为⊙O的切线,又FD为⊙O的切线,
∴FD=CF,
∴AF=CF.(5分)
(Ⅱ)解:∵直角三角形FED中,ED=4,sin∠E=
,
∴cos∠E=
,
∴FE=5,(8分)
又FD=3=FC,
∴CE=2.(10分)
| π |
| 2 |
∴∠ADF+∠BDO=
| π |
| 2 |
又∵⊙O中OD=OB,
∴∠BDO=∠OBD,
∴∠ADF+∠OBD=
| π |
| 2 |
 在Rt△ABC中,
在Rt△ABC中,∴∠A+∠OBD=
| π |
| 2 |
∴AF=FD,
又在直角三角形ABC中,直角边BC为⊙O的直径,
∴AC为⊙O的切线,又FD为⊙O的切线,
∴FD=CF,
∴AF=CF.(5分)
(Ⅱ)解:∵直角三角形FED中,ED=4,sin∠E=
| 3 |
| 5 |
∴cos∠E=
| 4 |
| 5 |
∴FE=5,(8分)
又FD=3=FC,
∴CE=2.(10分)
点评:本题考查了切线的性质,解三角形等的综合运用.属于基础题.

练习册系列答案
相关题目
已知:在△ABC中,
=
,则此三角形为( )
| c |
| b |
| cosC |
| cosB |
| A、直角三角形 |
| B、等腰直角三角形 |
| C、等腰三角形 |
| D、等腰或直角三角形 |
