题目内容
已知函数y= (1)求![]() 的表达式;
的表达式;
(2)是否存在正实数p,使F(x)在(-∞,f(2)]上是增函数,在(f(2),0)上是减函数?
解析:(1)∵图象过点M(m-2,0),?
∴m-2是方程ax2-(a-3)x+(a-2)=0的解,即方程存在实根.?
∴Δ≥0.?
又Δ=[-(a-3)]2-4a(a-2)≥0,?
解得![]() .?
.?
∵a是负整数,∴a=-1.?
∴f(x-2)=-x2+4x-3=-(x-2)2+1.?
∴![]() =1-x2.?
=1-x2.?
(2)由上式f(2)=-3,g(x)=1-(1-x2)2=2x2-x4,F(x)=p(2x2-x4)-4(1-x2).?
假设存在正实数p使F(x)在(-∞,-3]上是增函数,在(-3,0)上是减函数,由于F(x)可导,∴F′(-3)=0且F′(x)=4(p+2)x-4px3.?
由F′(-3)=0,得p=![]() .而当p=
.而当p=![]() 时,F′(x)=-x(x+3)(x-3).?
时,F′(x)=-x(x+3)(x-3).?
∴当x<-3时,F′(x)>0,F(x)在(-∞,-3]上为增函数;?
当-3<x<0时,F′(x)<0,F(x)在(-3,0)上为减函数.?
综上,满足条件的p存在且p=![]() .
.

练习册系列答案
相关题目
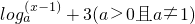 的图象恒过点P,若角α的终边经过点P,则cos2α-sin2α的值等于________.
的图象恒过点P,若角α的终边经过点P,则cos2α-sin2α的值等于________. ,其图象过点
,其图象过点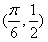 ,
,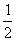 ,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在[0,
,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在[0,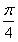 ]上的最大值和最小值.
]上的最大值和最小值. 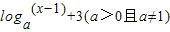 的图象恒过点P,若角α的终边经过点P,则cos2α-sin2α的值等于 .
的图象恒过点P,若角α的终边经过点P,则cos2α-sin2α的值等于 .