题目内容
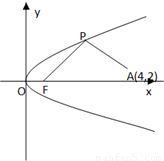
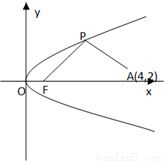
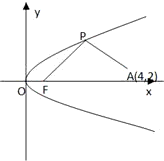 如图所示,F是抛物线y2=2px(p>0)的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点,|PA|+|PF|的最小值为8.
如图所示,F是抛物线y2=2px(p>0)的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点,|PA|+|PF|的最小值为8.
(1)求抛物线方程;
(2)若O为坐标原点,问是否存在点M,使过点M的动直线与抛物线交于B,C两点,且以BC为直径的圆恰过坐标原点,若存在,求出动点M的坐标;若不存在,请说明理由.
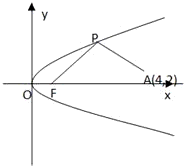 解:如图,设抛物线的准线为l,过P作PB⊥l于B,过A作AC⊥l于C,
解:如图,设抛物线的准线为l,过P作PB⊥l于B,过A作AC⊥l于C,(1)由抛物线定义知|PF|=|PB|?|PA|+|PF|=|PA|+|PB|≥|AC|(折线段大于垂线段),当且仅当A,P,C三点共线取等号.由题意知|AC|=8,即
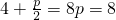 ?抛物线的方程为:y2=16x
?抛物线的方程为:y2=16x(2)假设存在点M,设过点M的直线方程为y=kx+b,
显然k≠0,b≠0,设B(x1,y1),C(x2,y2),由以BC为直径的圆恰过坐标
原点有
 ?x1x2+y1y2=0①
?x1x2+y1y2=0①把y=kx+b代入y2=16x得k2x2+2(bk-8)x+b2=0
由韦达定理
 .②
.②又y1y2=(kx1+b)(kx2+b)=k2x1x2+bk(x1+x2)+b2.③
②代入③得
 .④
.④②④代入①得
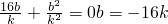 ?动直线方程为y=kx-16k=k(x-16)必过定点(16,0)
?动直线方程为y=kx-16k=k(x-16)必过定点(16,0)当kBC不存在时,直线x=16交抛物线于B(16,-16),C(16,16),仍然有
 ,
,综上:存在点M(16,0)满足条件.
分析:(1)如图,设抛物线的准线为l,过P作PB⊥l于B,过A作AC⊥l于C,由抛物线定义知当且仅当A,P,C三点共线取等号.由题意知|AC|=8,从而求得p值,最后写出抛物线的方程;
(2)假设存在点M,设过点M的直线方程为y=kx+b,对于存在性问题,可先假设存在,即假设存在点M,设过点M的直线方程为y=kx+b,再利用以BC为直径的圆恰过坐标
原点,求出点M的坐标,若出现矛盾,则说明假设不成立,即不存在;否则存在.
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生分析问题和解决问题的能力.当研究直线与圆锥曲线的关系的问题时,常可利用联立方程,进而利用韦达定理来解决.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 如图所示,F是抛物线y2=2px(p>0)的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点,|PA|+|PF|的最小值为8.
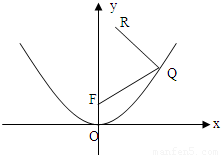
如图所示,F是抛物线y2=2px(p>0)的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点,|PA|+|PF|的最小值为8.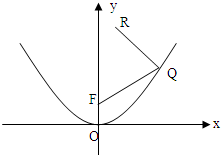 如图所示,F是抛物线x2=2py(p>0)的焦点,点R(1,4)为抛物线内一定点,点Q为抛物线上一动点,|QR|+|QF|的最小值为5.
如图所示,F是抛物线x2=2py(p>0)的焦点,点R(1,4)为抛物线内一定点,点Q为抛物线上一动点,|QR|+|QF|的最小值为5.