题目内容
(2012•海淀区二模)曲线C是平面内到定点A(1,0)的距离与到定直线x=-1的距离之和为3的动点P的轨迹.则曲线C与y轴交点的坐标是
.
(0,±
)
| 3 |
(0,±
)
;又已知点B(a,1)(a为常数),那么|PB|+|PA|的最小值d(a)=| 3 |
|
|
分析:(1)设动点P(x,y),由题意可得
+|x+1|=3.对x分类讨论:①当x<-4时,由|x+1|>3,无轨迹;②当-4≤x≤-1时,化为
=x+4,化为y2=10x+15(-1≥x≥-
),与y轴无交点;③当x>-1时,化为
=2-x,化为y2=-2x+3,(-1<x≤
),令x=0即可得出y.
(2)利用(1)画出图象,分类讨论求出即可.
| (x-1)2+y2 |
| (x-1)2+y2 |
| 3 |
| 2 |
| (x-1)2+y2 |
| 3 |
| 2 |
(2)利用(1)画出图象,分类讨论求出即可.
解答:解:(1)设动点P(x,y),由题意可得
+|x+1|=3,
①当x<-4时,∵|x+1|>3,无轨迹;
②当-4≤x≤-1时,化为
=x+4,化为y2=10x+15(-1≥x≥-
),与y轴无交点;
③当x>-1时,化为
=2-x,化为y2=-2x+3,(-1<x≤
).
令x=0,解得y=±
.
综上①②③可知:曲线C与y轴的交点为(0,±
);
(2)由(1)可知:y2=
.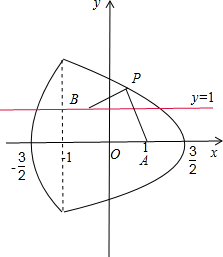
如图所示,令y=1,则10x+15=1,或-2x+3=1,
解得x=-1.4或1.
①当a≤-1.4或a≥1时,|PA|+|PB|≥|AB|,∴d(a)=|AB|=
=
;
②当-1<a<1时,当直线y=1与y2=-2x+3(-1<x≤
)相交时的交点P满足|PA|+|PB|取得最小值,
∵此抛物线的准线为x=2,∴直线y=1与准线的交点Q(2,1),此时d(a)=|QB|=2-a;
③当-1.4<a≤-1时,当直线y=1与y2=10x+15(-
≤x≤-1)相交时的交点P满足|PA|+|PB取得最小值,
∵此抛物线的准线为x=-4,∴直线y=1与准线的交点Q(-4,1),此时d(a)=|QB|=a+4.
综上可知:d(a)=
| (x-1)2+y2 |
①当x<-4时,∵|x+1|>3,无轨迹;
②当-4≤x≤-1时,化为
| (x-1)2+y2 |
| 3 |
| 2 |
③当x>-1时,化为
| (x-1)2+y2 |
| 3 |
| 2 |
令x=0,解得y=±
| 3 |
综上①②③可知:曲线C与y轴的交点为(0,±
| 3 |
(2)由(1)可知:y2=
|

如图所示,令y=1,则10x+15=1,或-2x+3=1,
解得x=-1.4或1.
①当a≤-1.4或a≥1时,|PA|+|PB|≥|AB|,∴d(a)=|AB|=
| (a-1)2+1 |
| a2-2a+2 |
②当-1<a<1时,当直线y=1与y2=-2x+3(-1<x≤
| 3 |
| 2 |
∵此抛物线的准线为x=2,∴直线y=1与准线的交点Q(2,1),此时d(a)=|QB|=2-a;
③当-1.4<a≤-1时,当直线y=1与y2=10x+15(-
| 3 |
| 2 |
∵此抛物线的准线为x=-4,∴直线y=1与准线的交点Q(-4,1),此时d(a)=|QB|=a+4.
综上可知:d(a)=
|
点评:本题综合考查了抛物线的定义、方程及其性质、直线与抛物线相交问题转化为方程联立得到根与系数的关系、两点间的距离公式等基础知识与基本技能,考查了分类讨论的思想方法、推理能力和计算能力.

练习册系列答案
相关题目