题目内容
已知定义域为R的奇函数y=f(x)在(0,+∞)是减函数,且f(1)=0,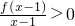 的解集为________(结果用区间表示).
的解集为________(结果用区间表示).
(0,1)∪(1,2)
分析:先由函数的奇偶性、单调性画出f(x)的草图,结合图象对不等式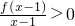 进行等价转化,从而可解.
进行等价转化,从而可解.
解答:∵f(x)是定义域为R的奇函数,且在(0,+∞)上是减函数,
∴在(-∞,0)上也是减函数;
又因为f(-1)=-f(1)=0.
可得其大致图象,如右图:结合图象可得
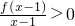 ?
? 或
或
? ,
,
解得,1<x<2或0<x<1.
故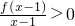 的解集为:(1,2)∪(0,1).
的解集为:(1,2)∪(0,1).
故答案为:(1,2)∪(0,1).
点评:本题考查抽象函数的单调性、奇偶性,及抽象不等式的求解,解抽象不等式一般借助函数的单调性解决.
分析:先由函数的奇偶性、单调性画出f(x)的草图,结合图象对不等式
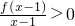 进行等价转化,从而可解.
进行等价转化,从而可解.解答:∵f(x)是定义域为R的奇函数,且在(0,+∞)上是减函数,
∴在(-∞,0)上也是减函数;

又因为f(-1)=-f(1)=0.
可得其大致图象,如右图:结合图象可得
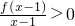 ?
? 或
或
?
 ,
,解得,1<x<2或0<x<1.
故
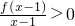 的解集为:(1,2)∪(0,1).
的解集为:(1,2)∪(0,1).故答案为:(1,2)∪(0,1).
点评:本题考查抽象函数的单调性、奇偶性,及抽象不等式的求解,解抽象不等式一般借助函数的单调性解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目