题目内容
如图,正四棱柱ABCD-A B
B C
C D
D 中,底面边长为2
中,底面边长为2 ,侧棱长为4,点E、F分别为棱AB、BC的中点,EF∩BD=G,求点D
,侧棱长为4,点E、F分别为棱AB、BC的中点,EF∩BD=G,求点D 到平面B
到平面B EF的距离d。
EF的距离d。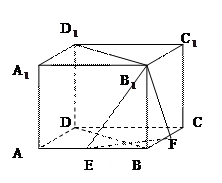
 B
B C
C D
D 中,底面边长为2
中,底面边长为2 ,侧棱长为4,点E、F分别为棱AB、BC的中点,EF∩BD=G,求点D
,侧棱长为4,点E、F分别为棱AB、BC的中点,EF∩BD=G,求点D 到平面B
到平面B EF的距离d。
EF的距离d。

点D 到平面EFB
到平面EFB 的距离为
的距离为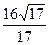
 到平面EFB
到平面EFB 的距离为
的距离为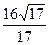
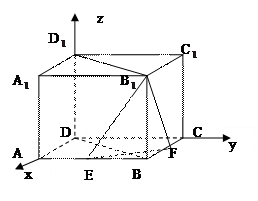
如图,建立空间直角坐标系D-xyz。易得D (0,0,4),B
(0,0,4),B (2
(2 ,2
,2 ,4),
,4),
E(2 ,
, ,0),F(
,0),F( ,2
,2 ,0),
,0),
故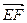 =(-
=(- ,
, ,0),
,0),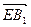 =(0,
=(0, ,4),
,4),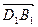 =(2
=(2 ,2
,2 ,0),
,0),
设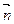 =(x,y,z)是平面B
=(x,y,z)是平面B EF的法向量,
EF的法向量,
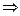
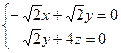 ,令x=1,得
,令x=1,得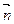 =(1,1,-
=(1,1,-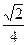 )。则|
)。则|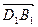 ·
·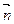 |=4
|=4 ,∴d=
,∴d= 。
。
故点D 到平面EFB
到平面EFB 的距离为
的距离为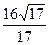 。
。
 (0,0,4),B
(0,0,4),B (2
(2 ,2
,2 ,4),
,4),E(2
 ,
, ,0),F(
,0),F( ,2
,2 ,0),
,0),故
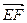 =(-
=(- ,
, ,0),
,0),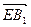 =(0,
=(0, ,4),
,4),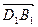 =(2
=(2 ,2
,2 ,0),
,0),设
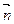 =(x,y,z)是平面B
=(x,y,z)是平面B EF的法向量,
EF的法向量,
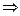
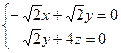 ,令x=1,得
,令x=1,得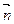 =(1,1,-
=(1,1,-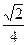 )。则|
)。则|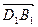 ·
·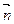 |=4
|=4 ,∴d=
,∴d= 。
。故点D
 到平面EFB
到平面EFB 的距离为
的距离为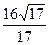 。
。
练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
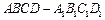 中,点
中,点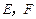 分别在
分别在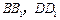 上,且
上,且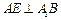 ,
,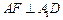 .
.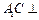 平面
平面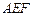 ;
;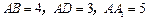 时,求平面
时,求平面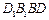 所成角的大小.
所成角的大小.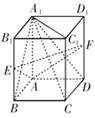
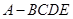 中,平面
中,平面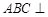 平面
平面 ;
;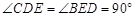 ,
, ,
,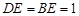 ,
,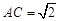 .
.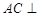 平面
平面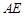 与平面
与平面 所成的角的正切值.
所成的角的正切值.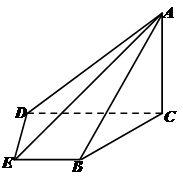
 为等边三角形,且
为等边三角形,且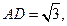
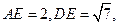 点F为棱BE上的动点。
点F为棱BE上的动点。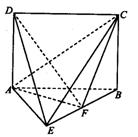
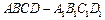 中,
中,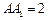 ,底面
,底面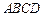 是直角梯形,
是直角梯形,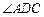 是直角,
是直角,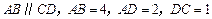 ,求异面直线
,求异面直线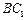 与
与 所成角的大小.
所成角的大小.
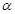 、
、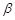 、
、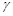 是三个不同的平面,给出下列命题,正确的是( ).
是三个不同的平面,给出下列命题,正确的是( ).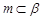 ,
,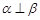 ,则
,则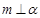
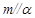 ,
,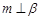 ,则
,则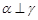 ,则
,则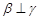
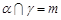 ,
,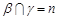 ,
, ,则
,则