题目内容
在正方体ABCD-A1B1C1D1中E是CC1的中点，过点E作一直线与直线A1D1和直线AB都相交，这样的直线（ ）
分析：先由不共线的三点E，A，B确定的平面进行延展，不共线的三点E，A1，D1确定的平面进行延展，如图，平面EAB与平面EA1D1的交线EA′即为与直线A1D1和直线AB都相交，根据EA′是两个平面的交线，从而得出正确选项．
解答：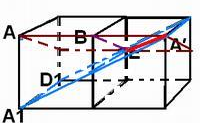
解：由不共线的三点E，A，B确定的平面进行延展，不共线的三点E，A1，D1确定的平面进行延展，
如图，平面EAB与平面EA1D1的交线EA′即为与直线A1D1和直线AB都相交，
因为EA′是两个平面的交线，故其惟一．
故选B．
解：由不共线的三点E，A，B确定的平面进行延展，不共线的三点E，A1，D1确定的平面进行延展，如图，平面EAB与平面EA1D1的交线EA′即为与直线A1D1和直线AB都相交，
因为EA′是两个平面的交线，故其惟一．
故选B．
点评：本小题主要考查空间中直线与直线之间的位置关系、异面直线的概念等基础知识，考查空间想象力、化归与转化思想．属于中档题．
练习册系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）