题目内容
下列命题中真命题的个数是( )①存在斜四棱柱,其底面为正方形;
②存在棱锥,其所有而均为直角三角形;
③任意的圆锥都存在两条母线互相垂直;
④任意的三棱柱都可以分割为三个体积相同的三棱锥.
A.1
B.2
C.3
D.4
【答案】分析:从四棱柱、三棱锥、圆锥、三棱柱,的定义和结构出发,逐一判断,注意特例即可.
解答: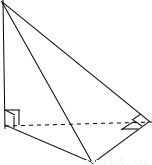 解:①存在斜四棱柱,其底面为正方形;正确.
解:①存在斜四棱柱,其底面为正方形;正确.
②存在棱锥,其所有而均为直角三角形;如图
③任意的圆锥都存在两条母线互相垂直;这是不正确的.
圆锥的顶角小于90°时就没有了.
④任意的三棱柱都可以分割为三个体积相同的三棱锥.
是正确的,三棱锥的体积公式就是这样推出的.
故选C
点评:本题考查学生的空间想象能力,考查学生的视图能力,判断能力,是中档题.
解答:
 解:①存在斜四棱柱,其底面为正方形;正确.
解:①存在斜四棱柱,其底面为正方形;正确.②存在棱锥,其所有而均为直角三角形;如图
③任意的圆锥都存在两条母线互相垂直;这是不正确的.
圆锥的顶角小于90°时就没有了.
④任意的三棱柱都可以分割为三个体积相同的三棱锥.
是正确的,三棱锥的体积公式就是这样推出的.
故选C
点评:本题考查学生的空间想象能力,考查学生的视图能力,判断能力,是中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目