题目内容
选修4-4：坐标系与参数方程在直角坐标系xOy中，直线l经过点P（-1，0），其倾斜角为α，以原点O为极点，以x轴非负半轴为极轴，与直角坐标系xOy取相同的长度单位，建立极坐标系．设曲线C的极坐标方程为ρ2-6ρcosθ+5=0．
（1）若直线l与曲线C有公共点，求α的取值范围；
（2）设M（x，y）为曲线C上任意一点，求x+y的取值范围．
【答案】分析：（1）先根据极坐标与直角坐标互化的公式，算出曲线C的直角坐标方程，再结合直线l的参数方程：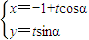
，联解得到关于参数t的二次方程，运用根的判别式列式并解之，即可得到角α的取值范围；
（2）由（1）可得曲线C的参数方程，从而得到x+y=3+2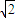
sin（θ+
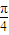），最后结合正弦函数的值域，即可得到x+y的取值范围．
解答：解：（1）将曲线ρ2-6ρcosθ+5=0化成直角坐标方程，得圆C：x2+y2-6x+5=0
直线l的参数方程为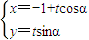
（t为参数）
将其代入圆C方程，得（-1+tcosα）2+（tsinα）2-6tsinα+5=0
整理，得t2-8tcosα+12=0
∵直线l与圆C有公共点，
∴△≥0，即64cos2α-48≥0，可得cosα≤-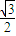
或cosα≥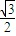
∵α为直线的倾斜角，得α∈[0，π）
∴α的取值范围为[0，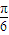
]∪[
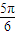，π）
（2）由圆C：x2+y2-6x+5=0化成参数方程，得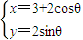
（θ为参数）
∵M（x，y）为曲线C上任意一点，
∴x+y=3+2cosθ+2sinθ=3+2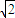
sin（θ+
）
∵sin（θ+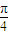
）∈[-1，1]
∴2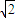
sin（θ+
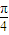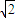）∈[-2
，2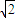
]，可得x+y的取值范围是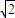[3-2
，3+2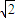
]．
点评：本题给出直线与圆的极坐标方程，要求我们将其化成直角坐标方程并研究直线与圆位置关系．着重考查了直角坐标与极坐标的互化、简单曲线的极坐标方程和直线与圆的位置关系等知识，属于中档题．
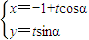，联解得到关于参数t的二次方程，运用根的判别式列式并解之，即可得到角α的取值范围；（2）由（1）可得曲线C的参数方程，从而得到x+y=3+2
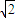sin（θ+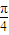），最后结合正弦函数的值域，即可得到x+y的取值范围．解答：解：（1）将曲线ρ2-6ρcosθ+5=0化成直角坐标方程，得圆C：x2+y2-6x+5=0
直线l的参数方程为
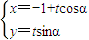（t为参数）将其代入圆C方程，得（-1+tcosα）2+（tsinα）2-6tsinα+5=0
整理，得t2-8tcosα+12=0
∵直线l与圆C有公共点，
∴△≥0，即64cos2α-48≥0，可得cosα≤-
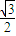或cosα≥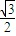∵α为直线的倾斜角，得α∈[0，π）
∴α的取值范围为[0，
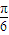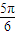]∪[，π）（2）由圆C：x2+y2-6x+5=0化成参数方程，得
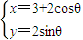（θ为参数）∵M（x，y）为曲线C上任意一点，
∴x+y=3+2cosθ+2sinθ=3+2
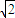sin（θ+）∵sin（θ+
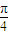）∈[-1，1]∴2
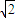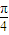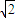sin（θ+）∈[-2，2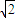]，可得x+y的取值范围是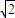[3-2，3+2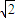]．点评：本题给出直线与圆的极坐标方程，要求我们将其化成直角坐标方程并研究直线与圆位置关系．着重考查了直角坐标与极坐标的互化、简单曲线的极坐标方程和直线与圆的位置关系等知识，属于中档题．
练习册系列答案
相关题目
A．选修4-1：几何证明选讲