题目内容
设函数 ,若关于
,若关于 的方程
的方程 恰有5个不同的实数解
恰有5个不同的实数解 ,则
,则 等于 (
)
等于 (
)
A.0 B.2lg2 C.3lg2 D.l
【答案】
C
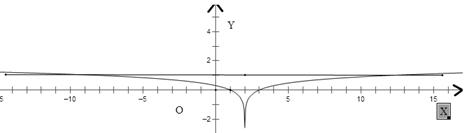
【解析】由题意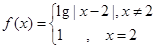 的图象如下,由图知y=1与函数
的图象如下,由图知y=1与函数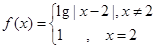 有三个交点,∵关于x的方程f2(x)+b f(x)+c=0恰有3个不同的实数解x1,x2,x3,∴若关于f(x)的一元二次函数仅有一个根为f(x)=1,由图象知,此时关于x的方程f2(x)+bf(x)+c=0恰有3个不同的实数解,由于函数的图象关于x=2对称,可关于f(x)的方程有两个不同的实数根,并且由一个实根为f(x)=1,此时关于x的方程f2(x)+bf(x)+c=0有五个不同的实数解,并且x1+x2+x3+x4+x5=10,所以
有三个交点,∵关于x的方程f2(x)+b f(x)+c=0恰有3个不同的实数解x1,x2,x3,∴若关于f(x)的一元二次函数仅有一个根为f(x)=1,由图象知,此时关于x的方程f2(x)+bf(x)+c=0恰有3个不同的实数解,由于函数的图象关于x=2对称,可关于f(x)的方程有两个不同的实数根,并且由一个实根为f(x)=1,此时关于x的方程f2(x)+bf(x)+c=0有五个不同的实数解,并且x1+x2+x3+x4+x5=10,所以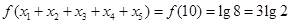 .
. 

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 ,若关于
,若关于 的方程
的方程 在
在 上恰好有两个相异实根,则实数
上恰好有两个相异实根,则实数 的取值范围为______________.
的取值范围为______________.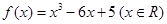 ,若关于
,若关于 的方程
的方程 有三个不同实根,则
有三个不同实根,则 的取值范围是( )
的取值范围是( )  (B)
(B)
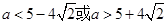 (D)
(D) 
 ,若关于
,若关于 的方程
的方程 有三个不同实根,则
有三个不同实根,则 的取值范围是______________ 。
的取值范围是______________ 。  ,若关于
,若关于 的方程
的方程 有三个不同实根,则
有三个不同实根,则 的取值范围是
.
的取值范围是
.