题目内容
抛物线的顶点在原点,对称轴是x轴,抛物线上点(-5,m)到焦点距离是6,则抛物线的方程是
- A.y 2=-2x
- B.y 2=-4x
- C.y 2=2x
- D.y 2=-4x或y 2=-36x
B
试题分析:因为抛物线的顶点在原点,对称轴是x轴,抛物线上点(-5,m)到焦点距离是6,所以可设抛物线方程为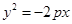 ,其焦点为(
,其焦点为(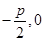 ),准线为
),准线为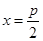 ,那么由抛物线定义知(-5,m)到焦点距离是6,即(-5,m)到准线距离是6,所以
,那么由抛物线定义知(-5,m)到焦点距离是6,即(-5,m)到准线距离是6,所以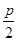 +5=6,
+5=6,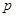 =2,y 2=-4x,故选B。
=2,y 2=-4x,故选B。
考点:本题主要考查抛物线的定义、标准方程、几何性质。
点评:明确抛物线的焦点、准线,将“抛物线上点(-5,m)到焦点距离是6”转化为“(-5,m)到准线距离是6”是简化解题过程的关键。
试题分析:因为抛物线的顶点在原点,对称轴是x轴,抛物线上点(-5,m)到焦点距离是6,所以可设抛物线方程为
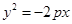 ,其焦点为(
,其焦点为(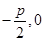 ),准线为
),准线为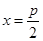 ,那么由抛物线定义知(-5,m)到焦点距离是6,即(-5,m)到准线距离是6,所以
,那么由抛物线定义知(-5,m)到焦点距离是6,即(-5,m)到准线距离是6,所以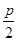 +5=6,
+5=6,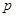 =2,y 2=-4x,故选B。
=2,y 2=-4x,故选B。考点:本题主要考查抛物线的定义、标准方程、几何性质。
点评:明确抛物线的焦点、准线,将“抛物线上点(-5,m)到焦点距离是6”转化为“(-5,m)到准线距离是6”是简化解题过程的关键。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
设抛物线的顶点在原点,准线方程为x=-2,则抛物线的方程是( )
| A、y2=-8x | B、y2=8x | C、y2=-4x | D、y2=4x |
 (2012•江苏一模)本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.
(2012•江苏一模)本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力. 实轴长为
实轴长为