题目内容
如图,菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3
.

(1)求证:OM∥平面ABD;
(2)求证:平面ABC⊥平面MDO;
(3)求三棱锥D-ABC的体积.
| 2 |

(1)求证:OM∥平面ABD;
(2)求证:平面ABC⊥平面MDO;
(3)求三棱锥D-ABC的体积.
分析:(1)利用菱形ABCD的特点,证明OM
AB,然后利用直线与平面平行的判定定理证明OM∥平面ABD;
(2)先证明OD⊥OM.OD⊥AC.OM∩AC=O,证明OD⊥平面ABC,然后证明平面ABC⊥平面MDO.
(3)判断OD为三棱锥D-ABC的高,求出S△ABC,然后求解三棱锥的体积.
| ∥ |
. |
| 1 |
| 2 |
(2)先证明OD⊥OM.OD⊥AC.OM∩AC=O,证明OD⊥平面ABC,然后证明平面ABC⊥平面MDO.
(3)判断OD为三棱锥D-ABC的高,求出S△ABC,然后求解三棱锥的体积.
解答:解:(1)证明:因为点O是菱形ABCD的对角线的交点,
所以O是AC的中点,又M是棱BC的中点,
所以OM是△ABC的中位线,OM
AB,
因为OM?平面ABD,AB?平面ABD,
所以OM∥平面ABD;
(2)证明:由题意,OM=OD=3,
因为DM=3
,所以∠DOM=90°,OD⊥OM.
又因为菱形ABCD,所以OD⊥AC.
因为OM∩AC=O,
所以OD⊥平面ABC,
因为OD?平面MDO,
所以平面ABC⊥平面MDO.
(3)解:由(Ⅱ)知,OD⊥平面ABC,
所以OD=3为三棱锥D-ABC的高,
因为菱形ABCD的边长为6,∠BAD=60°,
所以S△ABC=
×62=9
,
所以所求三棱锥的体积为V,V=
×9
×3=9
.
即三棱锥D-ABC的体积9
.
所以O是AC的中点,又M是棱BC的中点,
所以OM是△ABC的中位线,OM
| ∥ |
. |
| 1 |
| 2 |
因为OM?平面ABD,AB?平面ABD,
所以OM∥平面ABD;
(2)证明:由题意,OM=OD=3,
因为DM=3
| 2 |
又因为菱形ABCD,所以OD⊥AC.
因为OM∩AC=O,
所以OD⊥平面ABC,
因为OD?平面MDO,
所以平面ABC⊥平面MDO.
(3)解:由(Ⅱ)知,OD⊥平面ABC,
所以OD=3为三棱锥D-ABC的高,
因为菱形ABCD的边长为6,∠BAD=60°,
所以S△ABC=
| ||
| 4 |
| 3 |
所以所求三棱锥的体积为V,V=
| 1 |
| 3 |
| 3 |
| 3 |
即三棱锥D-ABC的体积9
| 3 |
点评:本题考查平面与平面垂直的判定,棱柱、棱锥、棱台的体积,直线与平面平行的判定,考查基本知识的灵活运用,逻辑推理能力与计算能力.

练习册系列答案
相关题目
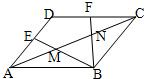 如图,菱形ABCD的边长为1,有∠D=120°,点E、F分别是AD、DC的中点,BE、BF分别与AC交于点M、N.
如图,菱形ABCD的边长为1,有∠D=120°,点E、F分别是AD、DC的中点,BE、BF分别与AC交于点M、N. (2011•西城区二模)如图,菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,
(2011•西城区二模)如图,菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点, 如图,菱形ABCD的边长为4,∠BAD=60°,AC∪BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=2
如图,菱形ABCD的边长为4,∠BAD=60°,AC∪BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=2 如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM= 如图,菱形ABCD的边长为2,∠A=60°,M为DC的中点,若N为菱形内任意一点(含边界),则
如图,菱形ABCD的边长为2,∠A=60°,M为DC的中点,若N为菱形内任意一点(含边界),则