题目内容
(本小题满分14分)
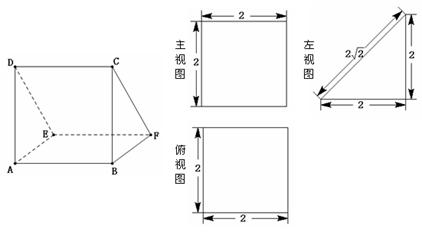
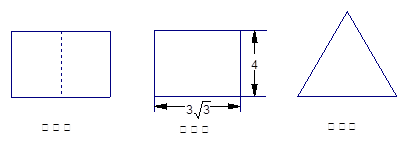
如图,已知 ⊥平面
⊥平面 ,
, ∥
∥ ,
, =1,且
=1,且 是
是 的中点.
的中点.

(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求证:平面BCE⊥平面 ;
;
(III) 求此多面体的体积.
如图,已知
 ⊥平面
⊥平面 ,
, ∥
∥ ,
, =1,且
=1,且 是
是 的中点.
的中点.

(Ⅰ)求证:
 ∥平面
∥平面 ;
;(Ⅱ)求证:平面BCE⊥平面
 ;
;(III) 求此多面体的体积.
(Ⅰ)(II)见解析;(III) 。
。
 。
。第一问在平面BCE中找一条直线BP(P是CE中点)与直线AF平行,由线面平行的判定定理可以得到证明;第二问先证AF,BP分别垂直于平面CDE,利用面面垂直的判定定理可以得到证明;第三问先找到高与底面然后求出体积。
解:(Ⅰ)取CE中点P,连结FP、BP,∵F为CD的中点, ∴FP∥DE,且FP=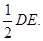 ---1分 又AB∥DE,且AB=
---1分 又AB∥DE,且AB=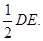 ∴AB∥FP,且AB=FP,---2分∴ABPF为平行四边形,∴AF∥BP. …………3分
∴AB∥FP,且AB=FP,---2分∴ABPF为平行四边形,∴AF∥BP. …………3分
又∵AF 平面BCE,BP
平面BCE,BP ∴AF∥平面BCE …………5分
∴AF∥平面BCE …………5分
(Ⅱ)∵ ,所以△ACD为正三角形,∴AF⊥CD—6分
,所以△ACD为正三角形,∴AF⊥CD—6分
∵AB⊥平面ACD,DE//AB ∴DE⊥平面ACD ----7分
又AF 平面ACD∴DE⊥AF 又AF⊥CD,CD∩DE=D∴AF⊥平面CDE
平面ACD∴DE⊥AF 又AF⊥CD,CD∩DE=D∴AF⊥平面CDE
又BP∥AF ∴BP⊥平面CDE-------9分
又∵BP 平面BCE ∴平面BCE⊥平面CDE …10分
平面BCE ∴平面BCE⊥平面CDE …10分
(III)此多面体是一个以C为定点,以四边形ABED为底边的四棱锥,
 ,----------12分
,----------12分
 等边三角形AD边上的高就是四棱锥的高---13分
等边三角形AD边上的高就是四棱锥的高---13分
 …………14分
…………14分
解:(Ⅰ)取CE中点P,连结FP、BP,∵F为CD的中点, ∴FP∥DE,且FP=
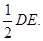 ---1分 又AB∥DE,且AB=
---1分 又AB∥DE,且AB=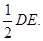 ∴AB∥FP,且AB=FP,---2分∴ABPF为平行四边形,∴AF∥BP. …………3分
∴AB∥FP,且AB=FP,---2分∴ABPF为平行四边形,∴AF∥BP. …………3分又∵AF
 平面BCE,BP
平面BCE,BP ∴AF∥平面BCE …………5分
∴AF∥平面BCE …………5分(Ⅱ)∵
 ,所以△ACD为正三角形,∴AF⊥CD—6分
,所以△ACD为正三角形,∴AF⊥CD—6分∵AB⊥平面ACD,DE//AB ∴DE⊥平面ACD ----7分
又AF
 平面ACD∴DE⊥AF 又AF⊥CD,CD∩DE=D∴AF⊥平面CDE
平面ACD∴DE⊥AF 又AF⊥CD,CD∩DE=D∴AF⊥平面CDE 又BP∥AF ∴BP⊥平面CDE-------9分
又∵BP
 平面BCE ∴平面BCE⊥平面CDE …10分
平面BCE ∴平面BCE⊥平面CDE …10分(III)此多面体是一个以C为定点,以四边形ABED为底边的四棱锥,
 ,----------12分
,----------12分 等边三角形AD边上的高就是四棱锥的高---13分
等边三角形AD边上的高就是四棱锥的高---13分 …………14分
…………14分
练习册系列答案
相关题目

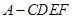 的体积为 .
的体积为 .