题目内容

如图2-5-15,PA切⊙O于A,PCB、PDE为⊙O的割线,并且PDE过圆心O,已知∠BPA＝30°,PA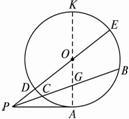＝,PC＝1,求PD的长.

图2-5-15

思路分析:求PD,可使用割线定理?PC·PB＝PD·PE,显然PA切⊙O,∴PA2＝PC·PB.?

可求得PB,但PE ＝PD +DE,DE为⊙O直径,所以求⊙O的直径成为解题的关键.

解:∵PA切⊙O于A,?

∴PA2＝PC·PB.?

又PB＝PC+BC,?

∴BC＝11.?

连结AO,并延长与⊙O交于K,与CB交于G,?

则GA＝PA  tan∠GPA＝PA tan30°＝2.?

又Rt△GPA中,∠GPA＝30°,?

∴PG ＝2GA ＝4.∴CG ＝3,GB ＝8.?

由相交弦定理GC·GB ＝AG·GK,可得GK＝12,?

∴直径为14.?

∴由割线定理有PC·PB＝PD·PE,得PD ＝-7.

练习册系列答案
相关题目
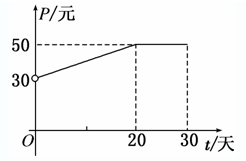根据市场调查，某种新产品投放市场的30天内，每件销售价格P（元）与时间t（天）的关系如图所示，日销售量Q（件）与时间t（天）之间的关系如表所示．
t/天 5 15 20 30
Q/件 35 25 20 10
（1）根据图象，写出该产品每件销售价格P与时间t的函数解析式；
（2）在所给的直角坐标系中，根据表中提供的数据描出实数对（t，Q）的对应点，并确定日销售量Q与时间t的一个函数解析式；
（3）在这30天内，哪一天的日销售金额最大？（日销售金额=每件产品销售价格×日销售量）
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分，请在答题纸指定区域内作答，解答应写出文字说明、证明过程或演算步骤．
A．选修4-1：（几何证明选讲）
如图，从O外一点P作圆O的两条切线，切点分别为A，B，
AB与OP交于点M，设CD为过点M且不过圆心O的一条弦，
求证：O，C，P，D四点共圆．
B．选修4-2：（矩阵与变换）
已知二阶矩阵M有特征值λ=3及对应的一个特征向量e1=[
 
1
1
]，并且矩阵M对应的变换将点（-1，2）变换成（9，15），求矩阵M．
C．选修4-4：（坐标系与参数方程）
在极坐标系中，曲线C的极坐标方程为p=2
2
sin（θ-
π
4
），以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
x=1+
4
5
t
y=-1-
3
5
t
（t为参数），求直线l被曲线C所截得的弦长．
D．选修4-5（不等式选讲）
已知实数x，y，z满足x+y+z=2，求2x2+3y2+z2的最小值．
（2006•嘉定区二模）某种商品在30天内每件的销售价格P（元）与时间t（天）的函数关系用如图中的两条线段表示；该商品在30天内的日销售量Q（件）与时间t（天）之间的关系如下表所示：
第t天 5 15 20 30
Q（件） 35 25 20 10
（1）根据提供的图象，写出该种商品每件的销售价格P与时间t的函数关系式，并根据表中数据确定日销售量Q与时间t的一个函数式；
（2）用y表示该商品的日销售金额，写出y关于t的函数关系式，求该商品的日销售金额的最大值，并指出日销售金额最大的一天是30天中的第几天？
如图2-15,⊙O的直径为10 cm,弦AB为8 cm,P是弦AB上一点,若OP的长为整数,则满足条件的点P有_____________个.(    )

图2-15

A.2                B.3                  C.4               D.5

如图2-5-15,⊙O1和⊙O2相交于点A、B,⊙O2和⊙O3相交于C、D,分别延长BA、DC相交于P,过P作⊙O1和⊙O3的切线PM、PN,M、N为切点,连结MN,求证:∠PMN=∠PNM.

图2-5-15

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网