题目内容
设椭圆的中心在坐标原点O,焦点在x轴上,离心率e=
| ||
| 2 |
| 2 |
分析:由于e=
,所以设椭圆方程为:
+
=1,设直线l方程为:y=kx+2,两者联立,又借助于△AOB的面积最大值为
,可化得:4S2k4+(4S2-16c2)k2+S2-8c2+32=0,从而S≤
,故问题得解.
| ||
| 2 |
| x2 |
| 2c2 |
| y2 |
| c2 |
| 2 |
| c2 | ||
|
解答:解:∵e=
,∴可设椭圆方程为:
+
=1,显然直线l的斜率存在,
设直线l方程为:y=kx+2,A(x1,y1),B(x2,y2)…1'
由
消去y整理,得(1+2k2)x2+8kx+8-2c2=0,
由韦达定理得,x1+x2=-
,x1x2=
…3′
∴S△AOB=
×2×|x1-x2|=
=
…6′
可化得:4S2k4+(4S2-16c2)k2+S2-8c2+32=0(*)…8'
∵k2有解,∴△=(4S2-16c2)2-4×4S2×(S2-8c2+32)≥0,
解得,S≤
…10'
∴Smin=
=
,∴c2=2,将c2=2,S=
代入(*)得,k=±
…13'
综上所述,椭圆方程为:
+
=1,直线l的方程为:y=±
x+2,…14'
| ||
| 2 |
| x2 |
| 2c2 |
| y2 |
| c2 |
设直线l方程为:y=kx+2,A(x1,y1),B(x2,y2)…1'
由
|
由韦达定理得,x1+x2=-
| 8k |
| 1+2k2 |
| 8-2c2 |
| 1+2k2 |
∴S△AOB=
| 1 |
| 2 |
| (x1+x2)2-4x1x2 |
|
可化得:4S2k4+(4S2-16c2)k2+S2-8c2+32=0(*)…8'
∵k2有解,∴△=(4S2-16c2)2-4×4S2×(S2-8c2+32)≥0,
解得,S≤
| c2 | ||
|
∴Smin=
| c2 | ||
|
| 2 |
| 2 |
| ||
| 2 |
综上所述,椭圆方程为:
| x2 |
| 4 |
| y2 |
| 2 |
| ||
| 2 |
点评:本题主要考查椭圆标准方程的求法、直线与圆锥曲线的综合问题.直线与圆锥曲线的综合题是高考的一个重点,每年必考.一般都是联立直线与圆锥曲线方程消去一个未知数,得到一元二次方程,表示出两根之和与两根之积,再结合题意来解.

练习册系列答案
相关题目
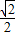 ,过椭圆外一点M(0,2)作直线l交椭圆与A,B两点,若△AOB的面积最大值为
,过椭圆外一点M(0,2)作直线l交椭圆与A,B两点,若△AOB的面积最大值为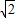 ,求此椭圆方程和直线l的方程.
,求此椭圆方程和直线l的方程.