题目内容
函数f(x)=1-2a-2acosx-2sin2x的最小值为g(a),a∈R,(1)求g(a);
(2)若g(a)=
 ,求a及此时f(x)的最大值.
,求a及此时f(x)的最大值.
【答案】分析:(1)利用同角三角函数间的基本关系化简函数解析式后,分三种情况:①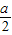 小于-1时②
小于-1时② 大于-1而小于1时③
大于-1而小于1时③ 大于1时,根据二次函数求最小值的方法求出f(x)的最小值g(a)的值即可;(2)把
大于1时,根据二次函数求最小值的方法求出f(x)的最小值g(a)的值即可;(2)把 代入到第一问的g(a)的第二和第三个解析式中,求出a的值,代入f(x)中得到f(x)的解析式,利用配方可得f(x)的最大值.
代入到第一问的g(a)的第二和第三个解析式中,求出a的值,代入f(x)中得到f(x)的解析式,利用配方可得f(x)的最大值.
解答:解:(1)f(x)=1-2a-2acosx-2(1-cos2x)
=2cos2x-2acosx-1-2a
=2(cosx-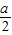 )2-
)2- -2a-1.
-2a-1.
若 <-1,即a<-2,则当cosx=-1时,f(x)有最小值g(a)=2(-1-
<-1,即a<-2,则当cosx=-1时,f(x)有最小值g(a)=2(-1-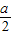 )2-
)2-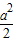 -2a-1=1;
-2a-1=1;
若-1≤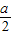 ≤1,即-2≤a≤2,则当cosx=
≤1,即-2≤a≤2,则当cosx= 时,f(x)有最小值g(a)=-
时,f(x)有最小值g(a)=-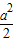 -2a-1;
-2a-1;
若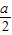 >1,即a>2,则当cosx=1时,f(x)有最小值g(a)=2(1-
>1,即a>2,则当cosx=1时,f(x)有最小值g(a)=2(1- )2-
)2-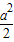 -2a-1=1-4a.
-2a-1=1-4a.
∴g(a)=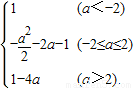
(2)若g(a)= ,由所求g(a)的解析式知只能是-
,由所求g(a)的解析式知只能是-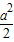 -2a-1=
-2a-1= 或1-4a=
或1-4a= .
.
由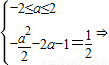 a=-1或a=-3(舍).由
a=-1或a=-3(舍).由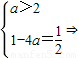 a=
a= (舍).
(舍).
此时f(x)=2(cosx+ )2+
)2+ ,得f(x)max=5.
,得f(x)max=5.
∴若g(a)= ,应a=-1,此时f(x)的最大值是5.
,应a=-1,此时f(x)的最大值是5.
点评:考查学生会利用二次函数的方法求三角函数的最值,要求学生掌握余弦函数图象的单调性.
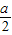 小于-1时②
小于-1时② 大于-1而小于1时③
大于-1而小于1时③ 大于1时,根据二次函数求最小值的方法求出f(x)的最小值g(a)的值即可;(2)把
大于1时,根据二次函数求最小值的方法求出f(x)的最小值g(a)的值即可;(2)把 代入到第一问的g(a)的第二和第三个解析式中,求出a的值,代入f(x)中得到f(x)的解析式,利用配方可得f(x)的最大值.
代入到第一问的g(a)的第二和第三个解析式中,求出a的值,代入f(x)中得到f(x)的解析式,利用配方可得f(x)的最大值.解答:解:(1)f(x)=1-2a-2acosx-2(1-cos2x)
=2cos2x-2acosx-1-2a
=2(cosx-
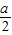 )2-
)2- -2a-1.
-2a-1.若
 <-1,即a<-2,则当cosx=-1时,f(x)有最小值g(a)=2(-1-
<-1,即a<-2,则当cosx=-1时,f(x)有最小值g(a)=2(-1-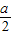 )2-
)2-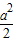 -2a-1=1;
-2a-1=1;若-1≤
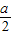 ≤1,即-2≤a≤2,则当cosx=
≤1,即-2≤a≤2,则当cosx= 时,f(x)有最小值g(a)=-
时,f(x)有最小值g(a)=-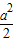 -2a-1;
-2a-1;若
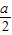 >1,即a>2,则当cosx=1时,f(x)有最小值g(a)=2(1-
>1,即a>2,则当cosx=1时,f(x)有最小值g(a)=2(1- )2-
)2-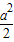 -2a-1=1-4a.
-2a-1=1-4a.∴g(a)=
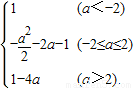
(2)若g(a)=
 ,由所求g(a)的解析式知只能是-
,由所求g(a)的解析式知只能是-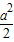 -2a-1=
-2a-1= 或1-4a=
或1-4a= .
.由
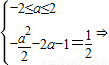 a=-1或a=-3(舍).由
a=-1或a=-3(舍).由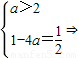 a=
a= (舍).
(舍).此时f(x)=2(cosx+
 )2+
)2+ ,得f(x)max=5.
,得f(x)max=5.∴若g(a)=
 ,应a=-1,此时f(x)的最大值是5.
,应a=-1,此时f(x)的最大值是5.点评:考查学生会利用二次函数的方法求三角函数的最值,要求学生掌握余弦函数图象的单调性.

练习册系列答案
相关题目