题目内容
选修4—5;不等式选讲
已知a和b是任意非零实数.
(1)求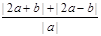 的最小值.
的最小值.
(2)若不等式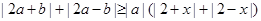 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.
【答案】
(I)最小值等于4. (II) 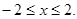
【解析】(I)根据绝对值不等式的性质可知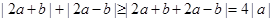 ,可得
,可得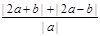 的最小值等于4.
的最小值等于4.
(II)先把不等式转化为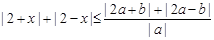 恒成立问题,然后根据第(I)的结论,进一步转化为
恒成立问题,然后根据第(I)的结论,进一步转化为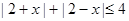 .解此不等式即可.
.解此不等式即可.
(I)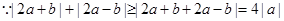 对于任意非零实数a和b恒成立,
对于任意非零实数a和b恒成立,
当且仅当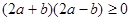 时取等号,
时取等号,
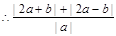 的最小值等于4.
的最小值等于4.
(II) 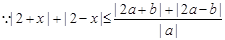 恒成立,
恒成立,
故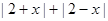 不大于
不大于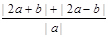 的最小值
的最小值
由(I)可知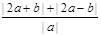 的最小值等于4.
的最小值等于4.
实数x的取值范围即为不等式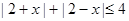 的解.
的解.
解不等式得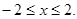

练习册系列答案
相关题目