Question

（08年江苏卷） 若，

且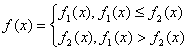

（1）求对所有实数成立的充要条件（用表示）

（2）设为两实数，且若

求证：在区间上的单调增区间的长度和为（闭区间的长度定义为）。

 

Answer 1

【解析】本小题考查充要条件、指数函数与绝对值、不等式的综合运用。

（1）由的定义可知，（对所有实数）等价于

（对所有实数）这又等价于，即

对所有实数均成立.        （*）

  由于的最大值为，

  故（*）等价于，即，这就是所求的充分必要条件

（2）分两种情形讨论

     （i）当时，由（1）知（对所有实数）

则由及易知，

再由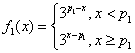的单调性可知，

函数在区间上的单调增区间的长度

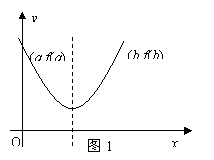
为（参见示意图1）

（ii）时，不妨设，则，于是

   当时，有，从而；

当时，有

从而  ；

当时，，及，由方程

      解得图象交点的横坐标为

                          ⑴

 

显然，

这表明在与之间。由⑴易知

 

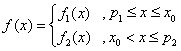
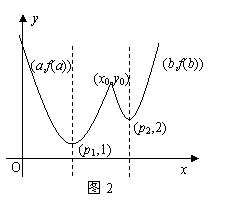
综上可知，在区间上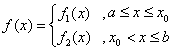，   （参见示意图2）

故由函数及的单调性可知，在区间上的单调增区间的长度之和为，由于，即，得

          ⑵

故由⑴、⑵得 

综合（i）（ii）可知，在区间上的单调增区间的长度和为。