题目内容
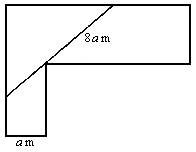
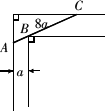
如图，宽为a的走廊与另一宽为b的走廊垂直相连，设细杆AC的长为l，∠ACD=α（1）试用a，b，α表示l；
（2）当b=a时，求当细杆AC能水平通过拐角时l的最大值；
（3）当l=8a时，问细杆AC能水平通过拐角，则另一走廊宽b至少是多少？
分析：（1）由AB=
，BC=
，可表示出l，注意角α范围；
（2）l=a(
+
)=
，令t=sinα+cosα=
sin（α+
），则l=a•
=
，t∈(1，
]，利用导数可求得l的最小值，从而可得答案；
（3）由（1）可得：b=8asinα-a•
，α∈(0，
)，利用导数可求得b的最小值；
| a |
| cosα |
| b |
| sinα |
（2）l=a(
| 1 |
| cosα |
| 1 |
| sinα |
| a(sinα+cosα) |
| sinαcosα |
| 2 |
| π |
| 4 |
| t | ||
|
| 2at |
| t2-1 |
| 2 |
（3）由（1）可得：b=8asinα-a•
| sinα |
| cosα |
| π |
| 2 |
解答：（解：（1）AB=
，BC=
，
∴l=AB+BC=
+
，∴l=
+
，α∈(0，
)；
（2）l=a(
+
)=
，
令t=sinα+cosα=
sin（α+
），
∵0＜α＜
，∴t∈(1，
]，sinαcosα=
，
∴l=a•
=
，t∈(1，
]，
而l′=
＜0，
∴l=
在t∈(1，
]上是减函数，且当t大于1且无限趋近于1时，l→+∞，∴l∈[4
，+∞），
∴细杆AC能水平通过拐角时l的最大值为4
．
（3）由（1）可得：b=8asinα-a•
，α∈(0，
)，
b′=8acosα-
=
=
，
令b′=0，则cosα=
，α=
，
当0＜α＜
时，b′＜0； 当
＜α＜
时，b′＞0，
∴当α=
时，bmin=3
a，
∴另一走廊的宽至少为3
a．
| a |
| cosα |
| b |
| sinα |
∴l=AB+BC=
| a |
| cosα |
| b |
| sinα |
| a |
| cosα |
| b |
| sinα |
| π |
| 2 |
（2）l=a(
| 1 |
| cosα |
| 1 |
| sinα |
| a(sinα+cosα) |
| sinαcosα |
令t=sinα+cosα=
| 2 |
| π |
| 4 |
∵0＜α＜
| π |
| 2 |
| 2 |
| t2-1 |
| 2 |
∴l=a•
| t | ||
|
| 2at |
| t2-1 |
| 2 |
而l′=
| -2a(1+t2) |
| (t2-1)2 |
∴l=
| 2at |
| t2-1 |
| 2 |
| 2 |
∴细杆AC能水平通过拐角时l的最大值为4
| 2 |
（3）由（1）可得：b=8asinα-a•
| sinα |
| cosα |
| π |
| 2 |
b′=8acosα-
| a |
| cos2α |
| a(8cos3α-1) |
| cos2α |
| a(2cosα-1)(4cos2α+2cosα+1) |
| cos2α |
令b′=0，则cosα=
| 1 |
| 2 |
| π |
| 3 |
当0＜α＜
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
∴当α=
| π |
| 3 |
| 3 |
∴另一走廊的宽至少为3
| 3 |
点评：本题考查导数在解决实际问题中的应用，考查导数求函数的最值，考查学生对题目的理解分析能力．
练习册系列答案
相关题目
