题目内容
 如图A、B是单位圆O上的点,且B在第二象限.C是圆与x轴正半轴的交点,A点的坐标为(
如图A、B是单位圆O上的点,且B在第二象限.C是圆与x轴正半轴的交点,A点的坐标为( ,
, ),△AOB为正三角形.
),△AOB为正三角形.(Ⅰ)求sin∠COA;
(Ⅱ)求cos∠COB.
【答案】分析:(Ⅰ)根据A的坐标,利用三角函数的定义直接求sin∠COA;
(Ⅱ)求出cosA,利用角的变换,化简cos∠COB=cos(∠COA+60°)展开,即可求cos∠COB.
解答:解:(Ⅰ)因为A点的坐标为 ,根据三角函数定义可知sin
,根据三角函数定义可知sin (4分)
(4分)
(Ⅱ)因为三角形AOB为正三角形,所以∠AOB=60°,
∵sin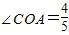 ,cos
,cos ,
,
所以cos∠COB=cos(∠COA+60°)=cos∠COAcos60°-sin∠COAsin60°= =
=
点评:本题是基础题,考查三角函数的定义,解答变换的技巧,两角和的余弦函数的应用,考查计算能力.
(Ⅱ)求出cosA,利用角的变换,化简cos∠COB=cos(∠COA+60°)展开,即可求cos∠COB.
解答:解:(Ⅰ)因为A点的坐标为
 ,根据三角函数定义可知sin
,根据三角函数定义可知sin (4分)
(4分)(Ⅱ)因为三角形AOB为正三角形,所以∠AOB=60°,
∵sin
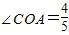 ,cos
,cos ,
,所以cos∠COB=cos(∠COA+60°)=cos∠COAcos60°-sin∠COAsin60°=
 =
=
点评:本题是基础题,考查三角函数的定义,解答变换的技巧,两角和的余弦函数的应用,考查计算能力.

练习册系列答案
相关题目
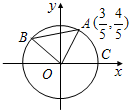 如图A,B是单位圆O上的点,且B在第二象限. C是圆与x轴正半轴的交点,A点的坐标为
如图A,B是单位圆O上的点,且B在第二象限. C是圆与x轴正半轴的交点,A点的坐标为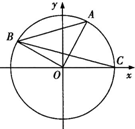 如图A.B是单位圆O上的点,且点B在第二象限. C是圆O与x轴正半轴的交点,A点的坐标为
如图A.B是单位圆O上的点,且点B在第二象限. C是圆O与x轴正半轴的交点,A点的坐标为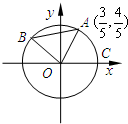 如图A、B是单位圆O上的点,且B在第二象限.C是圆与x轴正半轴的交点,A点的坐标为(
如图A、B是单位圆O上的点,且B在第二象限.C是圆与x轴正半轴的交点,A点的坐标为( 如图A,B是单位圆O上的点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形.若A点的坐标为(
如图A,B是单位圆O上的点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形.若A点的坐标为(