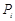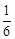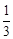题目内容
设离散型随机变量X的分布列为
|
X |
0 |
1 |
2 |
3 |
4 |
|
P |
0.2 |
0.1 |
0.1 |
0.3 |
m |
求:(Ⅰ)2X+1的分布列;
(Ⅱ)|X-1|的分布列.
【答案】
(Ⅰ)见解析(Ⅱ)见解析
【解析】本试题主要是考查了随机变量的分布列的求解的运用。
(1)根据已知x的分布列,对应的得到2x+1的概率值,从而得到相应的分布列。
(2)先分析得到|X-1|的可能取值,然后得到对应的概率值,写出分布列。
解 由分布列的性质知:
0.2+0.1+0.1+0.3+m=1,∴m=0.3.
首先列表为:
|
X |
0 |
1 |
2 |
3 |
4 |
|
2X+1 |
1 |
3 |
5 |
7 |
9 |
|
|X-1| |
1 |
0 |
1 |
2 |
3 |
从而由上表得两个分布列为:
(1)2X+1的分布列:
|
2X+1 |
1 |
3 |
5 |
7 |
9 |
|
P |
0.2 |
0.1 |
0.1 |
0.3 |
0.3 |
(2)|X-1|的分布列:
|
|X-1| |
0 |
1 |
2 |
3 |
|
P |
0.1 |
0.3 |
0.3 |
0.3 |

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
设离散型随机变量X的概率分布如下:
则X的均值为( )
| X | 0 | 1 | 2 | 3 | ||||||
| Pi |
|
|
|
p |
A、
| ||
B、
| ||
C、
| ||
D、
|